Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Surfaces integrals
1. Definitions and method
In three-dimetional space, we integreted, functions of two
variables or three variables, over a region D.
D could be rectangular or any region, but a plane region.
Now, in three-dementional space, we are now going to integrate
functions of three variables x, y, z, over some surface S .
The method is to link one of the three coordinates x, or, y , or
as a function the two others. That is x = g(y,z), y = g(x,z), or
z = g(x, z). Doing this leads to an integral over D, that
over a plane region D.
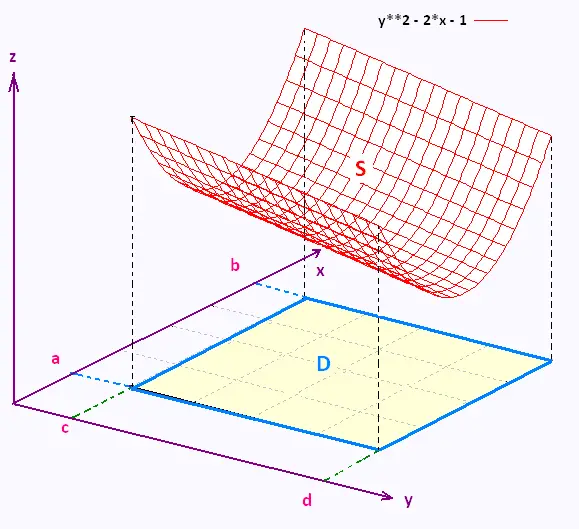
The region S lies above some region D that lies in the xy-plane.
The region D coud be rectangular, or any region. It could be in
front of the xy-plane, or the yz-plane or the xz-plane.
Let�s consider the surface integral in which the surface S is given by
z = f(x, y) . In this case the surface integral is:
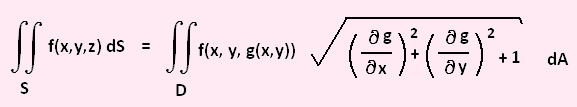
Note that the integral on the left is a surface integral with the
differential dS. The integral on the right is a double integral with
the differential dA.
With the parametric surfaces notation:
 (u,v) =
x(u,v) (u,v) =
x(u,v)  +
y(u,v) +
y(u,v)  + z(u,v) + z(u,v) 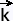 , ,
we use the following formula:
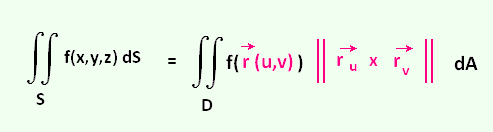
D is the set of the parameters u and v.
Example 1
Evaluate ∫∫S xy dS, where S is the portion of the plane
x + y + z = 2 that lies in the 1st octant and is in front of the yz-plane.
The equation of the surface in the form x = g(y,z) is:
x = g(y, z) = 2 - y - z
The integrand f(x,y,z) becomes: f(2 - y - z, y,z). So
the region D is the triangle of vertices (2,0), (0,0), and (0,2)
In the yz-plane, x = 0 z = 2 - y
The ranges for y and z are:
0 ≤ y ≤ 2 0 ≤ z ≤ 2 - y
√ [(∂g/∂y)2 + (∂g/∂z)2 + 1] =
=
√ [(- 1)2 + (- 1)2 + 1] = √3
Therefore
∫∫S xy dS =
∫∫D (2 - y - z)y √3 dA =
∫∫D (2y - y2 - zy) √3 dy dz =
√3 ∫02
∫02-y
(2y - y2 - zy)
dz dy
=
√3 ∫02
(2y - y2)(2 - y) - y(2 - y)2/2)
dy
= (y2 - (2/3)y3 + (1/8(y4)|02
= 2√/3.
∫∫S xy dS = 2√/3
Example 2
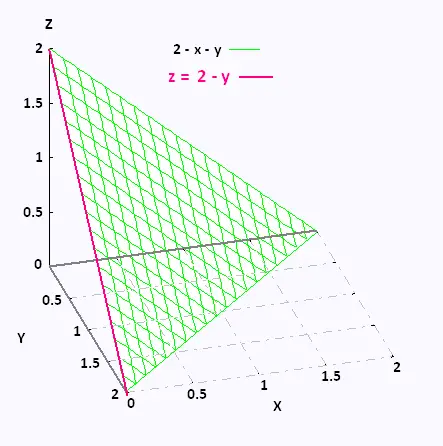
Evaluate ∫∫S x + y dS, where the surface S is the cylinder
x2 + y2 = 4 cut by a plane z = 3 - y.
We have:
∫∫S x + y dS = ∫∫S1 x + y dS +
∫∫S2 x + y dS +
∫∫S3 x + y dS
1. ∫∫S1 x + y dS
Parameterization of the cylinder:
• 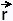 (z, φ) =
2 cos φ (z, φ) =
2 cos φ  +
2 sin φ +
2 sin φ 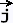 + z + z 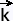
• 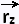 = ∂ = ∂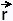 /∂z =
〈 0 , 0, 1 〉 /∂z =
〈 0 , 0, 1 〉
• 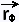 = ∂ = ∂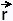 /∂φ =
〈 - 2 sin φ , 2 cos φ, 0 〉 /∂φ =
〈 - 2 sin φ , 2 cos φ, 0 〉
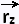 x x 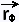 = = |
 |
 |
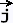 |
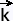 |
 |
| 0
|
0
|
1
|
| - 2 sin φ
|
2 cos φ
|
0
|
= √4 = 2.
• 0 ≤ θ ≤ 2π and
0 ≤ z ≤ 3 - y = 3 - 2 sin θ
Therefore
∫∫S1 x + y dS =
∫∫D (2 cos θ + 2 sin θ) (2) dA =
4 ∫02π
∫03-2sin θ (cos θ + sin θ) dz
dθ =
4 ∫02π
(cos θ + sin θ)(3 - 2 sin θ)
dθ =
4
(3 sin θ + cos (2θ) - 3 cos θ - θ +(1/2) sin (2))|02π
=
4 (- 2π) = - 8 π
∫∫S1 x + y dS = - 8 π
2. ∫∫S2 x + y dS
z = g(x, y) = 3 - y
√[(∂g/∂)2 + (∂g/∂)2 + 1] =
√[(0)2 + (- 1)2 + 1] = √2
∫∫S2 x + y dS =
∫02π
∫02
( r cos θ + r sin θ) (√2) r dr dθ =
(√2) ∫02π
∫02
r2 dr (cos θ + sin θ ) dθ =
(√2) ∫02π
(8/3) (cos θ + sin θ) dθ =
(8/3) (√2)
(sin θ - cos θ) |02π = 0
∫∫S2 x + y dS = 0
3. ∫∫S3 x + y dS
z = g(x, y) = 0
√[(∂g/∂)2 + (∂g/∂)2 + 1] =
√[(0)2 + (0)2 + 1] = √1 = 1.
∫∫S2 x + y dS =
∫02π
∫02
( r cos θ + r sin θ) r dr dθ =
∫02π
∫02
r2 dr (cos θ + sin θ) dθ =
(8/3) ∫02π
(cos θ + sin θ) dθ =
(8/3) ∫02π
(sin θ - cos θ) = 0
∫∫S3 x + y dS = 0
Therefore
∫∫S x + y dS = 0 - 8 π + 0 = - 8 π
∫∫S (x + y) dS = - 8 π
|
|