Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Tangent vectors
Normal vectors
We are going to determine the tangent and normal vectors
to level surfaces and parametric surfaces.
A level surface is defined by the equation: f(x,y,z) = k,
while parametric surface is defined by the position vector
 (u,v). (u,v).
1. Tangent and normal vectors
to level surfaces
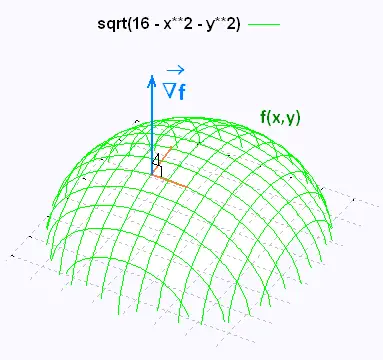
Consider a level surface defined by f(x,y,z) = k. The surface is said smooth if its gradient ∇f is continuous and non-zero at any point on the surface.
∇f = fx  +
fy +
fy  +
fz +
fz 
Let's suppose that  (t) = 〈 x(t), y(t), z(t)〉 lies on the smooth surface f(x,y,z) = k. (t) = 〈 x(t), y(t), z(t)〉 lies on the smooth surface f(x,y,z) = k.
Applying the derivative with respect to t to both sides of the equation of the
level surface yields:
df/dt = dk/dt
k is a constant, the chain rule implies that
df/dt =
(∂f/∂x)(∂x/∂t) + (∂f/∂y)(∂y/∂t) +
(∂f/∂xz)(∂z/∂t) =
= ∇f .  = dk/dt = 0 = dk/dt = 0
Where  = 〈 x', y', z' 〉 is the tangent vector to the surface at the
point = 〈 x', y', z' 〉 is the tangent vector to the surface at the
point  (x,y,z). (x,y,z).
∇f .  = 0 implies that the two
vectors ∇f and = 0 implies that the two
vectors ∇f and  are perpendicular.
So ∇f is orthogonal to each tangent vector are perpendicular.
So ∇f is orthogonal to each tangent vector  at a given point on the surface. at a given point on the surface.
Therefore
At a given point (x,y,z),
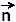 = ∇f(x,y,z)
is normal to the surface f(x,y,z) = k at the point (x,y,z). = ∇f(x,y,z)
is normal to the surface f(x,y,z) = k at the point (x,y,z).
Let's remember that:
The gradient ∇f is normal to the surface f(x,y, z) = k at
each point on the surface.
Exercice
Show, otherwise, that ∇f is orthogonal to
the level curve f(x,y,z) = k.
Let's consider a two-variables function f(x,y) and then
we will do an extension for the three-variable function f(x,y,z).
The differential of f(x,y) = k gives
df = (∂f/∂x)dx + (∂f/∂y)dy = dk = 0
That can be written as a dot product:
(∂f/∂x)dx + (∂f/∂y)dy = 〈fx,fy〉 . 〈dx, dy〉 =
∇f .  = 0 = 0
That is ∇f and  are orthogonal. are orthogonal.
We know that the vector  is tangent to the curve. So ∇f is normal to the curve. is tangent to the curve. So ∇f is normal to the curve.
The work for the level curve f(x,y,z) = k is identical. Then
The gradient ∇f is normal to the surface f(x,y,z) = k at
each point on the surface.
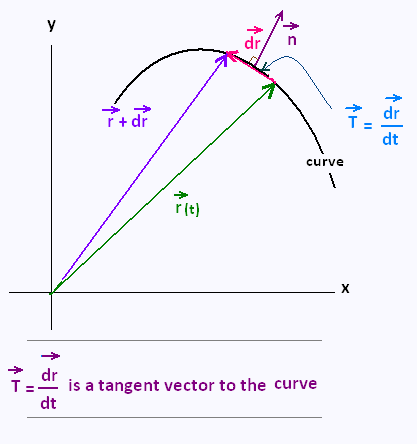
2. Tangent and normal vectors
to parametric surfaces
If we parameterize the fonction f(x,y,z) by the vector
 (u,v), then (u,v), then
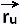 = ∂ = ∂ /∂u , and /∂u , and
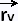 = ∂ = ∂ /∂v /∂v
are tangent to the surface.
Therefore their cross product 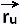 × ×
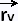 is normal to the surface. is normal to the surface.
Let's remember that:
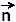 = = 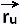 × ×
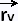 is normal to the surface. is normal to the surface.
|
|