Calculus III:
Spherical coodinates system
Volume element in spherical
coodinates system
Triple integrals in spherical coordinates
1. Using spherical coodinates system
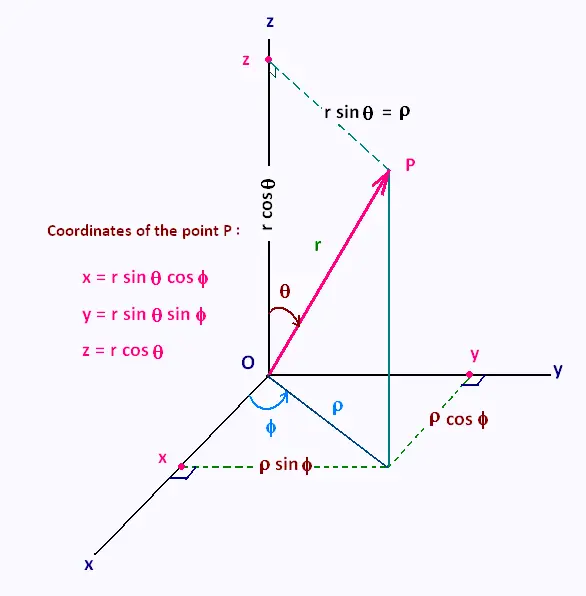
To integrate a three variables functions using the
spherical coordinates system, we then
restrict the region E down to a spherical wedge. That is:
a ≤ r ≤ b
α ≤ θ ≤ β
δ ≤ φ ≤ γ
2. The volume element in spherical
coodinates system
The volume element in spherical coodinates system is:
dV = r2 dr sin θ dθ dφ
3. The integral formula in spherical
coodinates system
The integral formula in spherical coodinates system is:
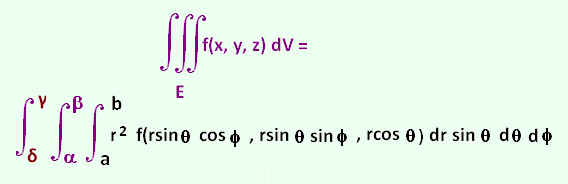
3.Examples
Example 1
Evaluate ∫∫∫E dV , where E is the sphere
x2 + y2 + z2 = R2.
Evaluate then the volume unit.
dV = dx dy dz = r2 dr sin θ dθ dφ
The region E is delimited by:
0 ≤ r ≤ R
0 ≤ θ ≤ π
0 ≤ φ ≤ 2π
Therefore:
∫∫∫E dV =
∫02π
∫0π
∫0R
r2 dr sin θ dθ dφ
∫01
r2 dr =
(r3/3)0R = R3/3
∫0π R3(1/3)
sin θ dθ =
(R3/3) ∫0π (
- cos θ)0π =
- (R3/3)(- 1 - 1) = 2R3/3
∫02π
2R3/3
dφ =
2π x (2R3/3) = 4R3π/3
Therefore:
∫∫∫E dV = (4π/3)R3
R = 1 gives the volume unit:
∫∫∫E dV = 4π/3
Example 2
Evaluate ∫∫∫E 2 z dV , where E is the upper half of
the sphere x2 + y2 + z2 = 1 .
dV = dx dy dz = r2 dr sin θ dθ dφ
The region E is delimited by:
0 ≤ r ≤ 1
0 ≤ θ ≤ π/2
0 ≤ φ ≤ 2π
Therefore:
∫∫∫E 2 z dV =
∫02π
∫0π/2
∫01
2 r cos θ r2 dr sin θ dθ dφ
∫01
2 r cos θ r2 dr = 2 cos θ ∫01
r3 dr =
2 cos θ
(r4/4)01 = (1/2) cos θ
∫0π/2 (1/2) cos θ
sin θ dθ =
(1/8) ∫0π/2
sin 2θ d2θ = - (1/8) (
cos 2θ)0π/2 =
= - (1/8)(- 1 - 1) = 1/4
∫02π
1/4
dφ =
2π x (1/4) = π/2
Therefore:
∫∫∫E 2 z dV = π/2
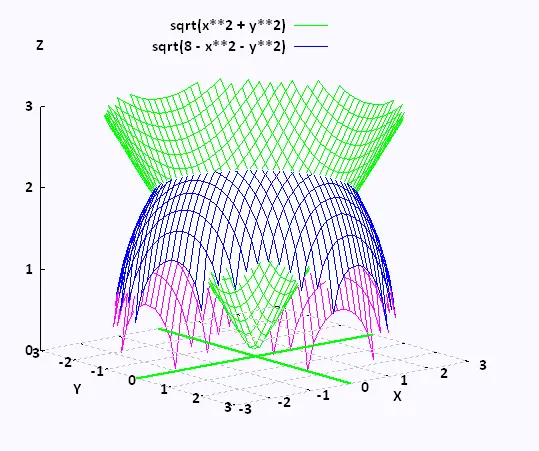
Example 3
Convert
∫01
∫0√(4 - y2)
∫√(x2 + y2)√(8 - x2 - y2)
(x2 + y2 + z2)
dz dx dy
into the integral in termes of spherical coordinates.
The limits for the variables are:
0 ≤ y ≤ 1
0 ≤ x ≤ √(4 - y2)
√(x2 + y2) ≤ z ≤ √(8 - x2 - y2)
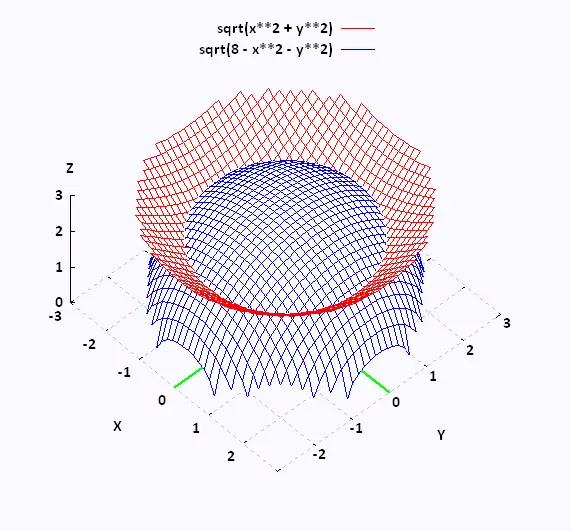
Notice that x2 + y2 + z2 = 8
is the 3D equation of the sphere of radius 2√2, and
z2 = x2 + y2
is the 3D equation of the cone.
The x's are positves, the y's are also positive. So the
region D is the quarter disk in the first quadrant of the xy-plane. that is :
0 ≤ φ ≤ π/2
The lower and upper bound for z are posives. So D is the first
octant.
The lower bound for z = √(x2 + y2). So
z2 = x2 + y2
The upper bound for z = √(8 - x2 - y2). So
z2 = 8 - x2 - y2. Or
x2 + y2 + z2 = 8. Hence
0 ≤ r ≤ √8 = 2√2
To determine θ we solve for where the cone and the sphere intersect:
x2 + y2 + z2 = 8
z2 + z2 = 8 → z = 2.
Since z = r cos θ. Then 2 = 2√2 cos θ → cos θ =
θ = π/4
The range for θ is then:
0 ≤θ ≤ π/4
Hence, the integral becomes:
∫02√2
∫0π/4
∫0π/2
r4 dr sin θ dθ dφ
|