Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Vector functions
Vector fields
Gradient vector field
Conservative vector fields
1. Definition
A vector field is a function vector  that assigns to each point
M in the space a vector that assigns to each point
M in the space a vector  (M). (M).
In two-dimension space,
M(x,y):  (M) = (M) =  (x,y). (x,y).
In three-dimension space,
if M(x,y,z): (M) = (M) =  (x,y,z). (x,y,z).
The standard notation of a vector field  (M) (M)
is built as :
• In two-dimention space:
 (M) = P(x,y) (M) = P(x,y)  + Q(x,y,z) + Q(x,y,z) 
• In three-dimention space:
 (M) = P(x,y,z) (M) = P(x,y,z) + Q(x,y,z) + Q(x,y,z) + R(x,y,z) + R(x,y,z)
2. Example
Let's sketch vector field  (M) =
- (x/2) (M) =
- (x/2) + (y/2) + (y/2) 
To graph the vector field, let's do evaluations.
•  (0, 0) = (0, 0) =
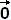
•  (1, - 1) = - (1/2) (1, - 1) = - (1/2) - (1/2) - (1/2)
At the point (1, - 1), we plot the vector
- (1/2) - (1/2) - (1/2) . .
•  (- 4, - 2) = 2 (- 4, - 2) = 2 - 1 - 1
At the point (- 4, - 2), we plot the vector
2 - -  . .
 (1, 2) =
- (1/2) (1, 2) =
- (1/2) + 1 + 1 . .
At the point (1, 2), we plot the vector
- (1/2) + +  . .
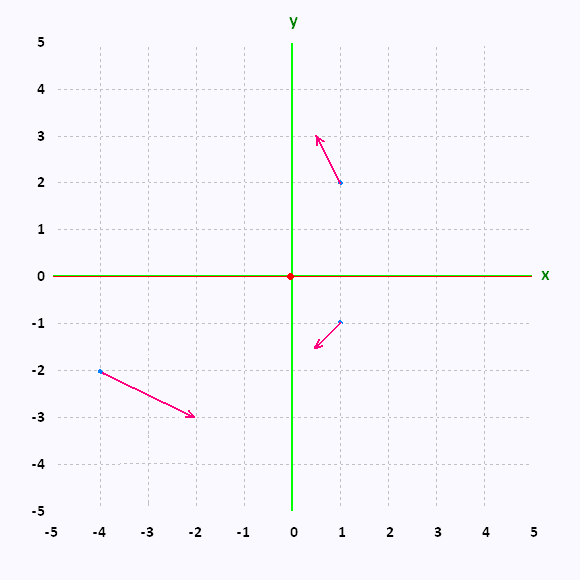
We can continue in this fashion plotting vectors for several points and we�ll get an almost complete sketch of the vector field.
3. The special case: The gradient vector
The special case of vector field function is the the gradient vector.
Given a function f(x, y, z), the gradient vector is written
∇f , and defined by:
∇f = fx +
fy +
fy +
fz +
fz
Where
fx = ∂f/∂x,
fy = ∂f/∂y, and
fz = ∂f/∂z,
Notice that f(x, y, z) is called scalar function .
For a two-variable function f(x,y), we just need to drop off the third component of the vector.
4. Conservative vector fields
A vector field is called a conservative vector field if there exists a function ƒ such that  = ∇ƒ. = ∇ƒ.
If  is a conservative vector field then the function, ƒ is called a potential function for is a conservative vector field then the function, ƒ is called a potential function for
 . .
That is, a vector field is conservative if it is a gradient vector field for some function.
Exemple
The vector field  = y = y + x + x is a conservative vector field with a potential function of ƒ(x, y) = xy. is a conservative vector field with a potential function of ƒ(x, y) = xy.
Indeed ∇ƒ = 〈 y, x 〉.
|
|