Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Vector functions
Calculus with vector functions
Limits of vector functions
Derivative of vector functions
Integral of vector functions
1. Limits
The limit of a vector function
 (t) = (f(t), g(t), h(t)) is defined as :
| lim(t) = | lim (f(t), | g(t), | h(t)) |
| t → a | t → a | |
| = | lim f(t) | lim g(t) | lim h(t) |
| | t → a | t → a | t → a |
| = | lim f(t) + | lim g(t) + | lim h(t) |
| | t → a | t → a | t → a |
We take the limit of each of the component's functions obtain a vector.
Example
Let's consider the following vector function:
(t) = (t2, t - 1, 2/t)
| lim(t) = | lim (t2, | t - 1, | 2/t) |
| t → 2 | t → 2 | |
| = | (lim t2 , | lim (t - 1) , | lim 2/t ) |
| | t → 2 | t → 2 | t → 2 |
| = | (4 , | 1 , | 2 ) |
| = | 4 + | + | 2 |
2. Derivatives
The derivative of a vector function
(t) = (f(t), g(t), h(t)) is defined as :
 (t) = 〈f'(t), g'(t), h'(t)〉
=
f'(t) + g'(t) + h'(t)
We have the following rules:
 |  +  ) =
| = ' + ' |
|
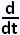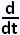| c) =
| c ' |
|
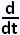| (f(t)) =
| = f'(t) + f(t)' |
|
| ( . ) =
| = '. + .' |
|
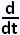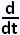| (x ) =
| = 'x + x' |
|
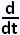| ((f(t)) =
| '(f(t)) f'(t) |
3. Integrals
• The indefinite integral of a vector function
(t) = (f(t), g(t), h(t)) is defined as :
∫
(t) = 〈
∫ f(t) dt,
∫ g(t)(t) dt,
∫ h(t)(t) dt
〉
+ 
=
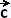∫ f(t) dt +
∫ g(t)(t) dt +
∫ h(t)(t)
+
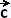
• For a definite integral of a vector function:
∫ab
(t) = 〈
∫ab f(t) dt,
∫ab g(t)(t) dt,
∫ab h(t)(t) dt
〉
=
∫ab f(t) dt +
∫ab g(t)(t) dt +
∫ab h(t)(t)
Example
The definite integral of the vector function:
(t) = (t2, t + 1, 3t)
from 0 to 2 is:
∫02
(t) =
(8/3) +
4 +
6
|
|