Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Vector operators
Hat operator
Part operator ∂
Del operator: Gradient and divergence
Curl Operator
Laplace Operator
1. Hat operator
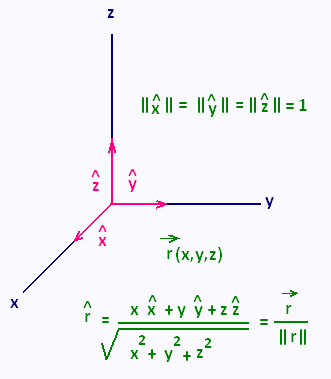
The Hat operator transforms a vector 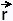 into
its unit vetor into
its unit vetor 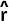 : :
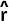 = = 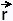 /|| /||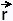 || ||
The unit vector has a magnitude of 1.
We have ||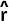 || = 1. || = 1.
2. Operator part: ∂
The vector partial: ∂ is defined as follows:
∂ = 〈 ∂/∂x, ∂/∂y, ∂/∂z 〉 = 〈 ∂x, ∂y, ∂z 〉
3. Del operator
By definition, It is written as:
∇ = 〈 ∂/∂x, ∂/∂y, ∂/∂z 〉 = ∂/∂xi
It acts on a scalar to give a vector. This is the gradient
of the scalar.
It acts on a vector to give a scalar. This is the divergence
of the scalar.
The Gradient:
∇ (scalar) = Vector
∇ φ = 〈 ∂φ/∂x, ∂φ/∂y,∂φ/∂z 〉
The result is a vector.
The Divergence:
∇ . (Vector) = Scalar ( dot product)
∇ . 〈 X, Y, Z 〉 =
〈 ∂/∂x, ∂/∂y, ∂/∂z〉 . 〈 X, Y, Z 〉 =
∂X/∂x + ∂Y/∂y + ∂Z/∂z
∇ . 〈X, Y, Z 〉 = ∂X/∂x + ∂Y/∂y + ∂Z/∂z
The result is a scalar.
4. Curl operator
∇ x (Vector) = Vector (cross product)
∇ x 〈 X, Y, Z 〉 =
〈 ∂/∂x, ∂/∂y, ∂/∂z 〉 x
〈 X, Y, Z 〉 =
〈
∂Z/∂y - ∂Y/∂z ,
∂ X/∂z - ∂Z/∂x ,
∂Y/∂x - ∂v/∂y 〉
∇ x ( X, Y, Z) =
〈
∂Z/∂y - ∂Y/∂z ,
∂X/∂z - ∂Z/∂x ,
∂Y/∂x - ∂X/∂y 〉
5. Laplacien operator
Δ ( Scalar) = Scalar
Δ = ∇2 = ∇ . ∇ =
〈 ∂2/∂x2, ∂2/∂y2, ∂2/∂z2〉 =
∇ . ∇ ( Scalar) = ∇ . Gradient = Divergence (Gradient)
Δ φ = ∂2φ/∂x2 + ∂2φ/∂y2 + ∂2φ/∂z2
|
|