Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Vector functions
Velocity and Acceleration
1. Velocity and Acceleration
Using vector functions, we will determine the velocity and acceleration of a moving object.
We already know, that given the position function of an object, the velocity of the object is the first derivative of the position function and the acceleration of the object is the second derivative of the position function.
So, the position function of an object is given by the vector function
 (t), and the velocity and acceleration of the object
are given by (t), and the velocity and acceleration of the object
are given by  (t), and (t), and 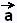 (t) (t)
To study of the motion of objects, the acceleration 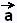 is often broken up into a tangential component (aT is often broken up into a tangential component (aT ), and a normal component (aN ), and a normal component (aN ) . ) .
The vectors  and and  are the unit tangent and unit normal for the position function.
are the unit tangent and unit normal for the position function.
The tangential component is the part of the acceleration that is tangential to the curve and the normal component is the part of the acceleration that is normal (or orthogonal) to the curve.
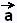 = aT = aT + aN + aN
2.Acceleration and curvature
The tangential and normal components of the acceleration are given by:
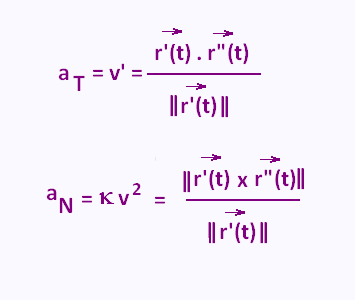
with v = || (t)||, and κ is the curvature for the position function. (t)||, and κ is the curvature for the position function.
Example 1
The acceleration of an object is given by
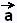 (t) =
2 (t) =
2 + 3 + 3 - 3t - 3t  . .
We want to determine the object's velocity and position functions given that the initial velocity is
 (0) = (0) =  - 2 - 2 ,
and the initial position is ,
and the initial position is  (0) =
3 (0) =
3 -
-  + 2 + 2
• The velocity is
 (t) = ∫ (t) = ∫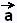 (t)dt = (t)dt =
∫ 2 dt + ∫ 3 dt + ∫ 3 dt -∫ 3t dt -∫ 3t  dt + dt + 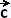 = =
2t + 3t + 3t - (3/2)t2 - (3/2)t2  + + 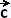
We use the initial velocity to determine the constant of integration 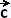 . .
We have :
 (0) = 2x0 (0) = 2x0 + 3x0 + 3x0 - (3/2)x02 - (3/2)x02  + + 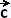 + + 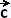 = =  +
+ 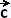
So
 (0) = (0) = 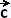 = =
 - 2 - 2
The velocity of the object is then:
 (t) =
2t (t) =
2t + 3t + 3t - (3/2)t2 - (3/2)t2  + + 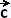 + +
 - 2 - 2 =
=
(2t+1) + 3t + 3t - ((3/2)t2 - 2) - ((3/2)t2 - 2) 
 (t) =
(2t+1) (t) =
(2t+1) + 3t + 3t - ((3/2)t2 - 2) - ((3/2)t2 - 2)
• We will find the position function by integrating the velocity function.
 (t) = ∫ (t) = ∫ (t) dt = (t) dt =
∫(2t+1) dt + ∫3t dt + ∫3t dt - ∫((3/2)t2 - 2) dt - ∫((3/2)t2 - 2)  dt = dt =
(t2 + t) +
(3/2)t2 +
(3/2)t2 - ((1/2)t3 - 2t) - ((1/2)t3 - 2t)  + + 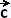
Using the initial position
 (0) =
(0 + 0) (0) =
(0 + 0) +
(3/2)(0) 2 +
(3/2)(0) 2 - ((1/2)(0)3 - 2(0)) - ((1/2)(0)3 - 2(0))  + + 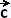
Therefore 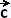 = =  (0) =
3 (0) =
3 -
-  + 2 + 2
So, the position function is:
 (t) =
(t2 + t) (t) =
(t2 + t) +
(3/2)t2 +
(3/2)t2 - ((1/2)t3 - 2t) - ((1/2)t3 - 2t)  + + 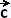 +
3 +
3 -
-  + 2 + 2 =
=
(t2 + t + 3) +
((3/2)t2 - 1) +
((3/2)t2 - 1) - ((1/2)t3 - 2t + 2) - ((1/2)t3 - 2t + 2) 
 (t) =
(t2 + t + 3) (t) =
(t2 + t + 3) +
((3/2)t2 - 1) +
((3/2)t2 - 1) - ((1/2)t3 - 2t + 2) - ((1/2)t3 - 2t + 2) 
Example 2
For the object in the previous example determine the tangential
and normal components of the acceleration.
 (t) = (t) =
(t2 + t + 3) +
((3/2)t2 - 1) +
((3/2)t2 - 1) - ((1/2)t3 - 2t + 2)
- ((1/2)t3 - 2t + 2) 
 (t) =
(2t + 1) (t) =
(2t + 1) +
(3t) +
(3t) - ((3/2)t2 - 2)
- ((3/2)t2 - 2) 
∥ (t)∥ = ∥
(2t + 1) (t)∥ = ∥
(2t + 1) +
(3t) +
(3t) - ((3/2)t2 - 2)
- ((3/2)t2 - 2)  ∥ = sqrt[2t + 1)2 + (3t)2 + (- ((3/2)t2 - 2))2]
∥ = sqrt[2t + 1)2 + (3t)2 + (- ((3/2)t2 - 2))2]
 (t)" =
2 (t)" =
2 +
3 +
3 - 3t
- 3t 
 (t) . (t) .  (t)" =
2(2t + 1) + 3(3t) + [- ((3/2)t2 - 2) (-3t)] =
4t + 2 + 9t + (9/2)t3 - 6t =
7t + 2 + (9/2)t3 (t)" =
2(2t + 1) + 3(3t) + [- ((3/2)t2 - 2) (-3t)] =
4t + 2 + 9t + (9/2)t3 - 6t =
7t + 2 + (9/2)t3
 (t) . (t) . "(t) =
(9/2)t3 + 7t + 2 "(t) =
(9/2)t3 + 7t + 2
 (t) x (t) x  "(t) = "(t) =
| (2t + 1) | (3t) | - ((3/2)t2 - 2) |
| 2 | 3 | - 3t |
= 3t(-3t) +3((3/2)t2 - 2) +
- 2((3/2)t2 - 2) + 3t(2t + 1) +
3(2t + 1) - 6t =
- (3/2)t2 + 3t + 1
 (t) x (t) x "(t) =
- (3/2)t2 + 3t + 1 "(t) =
- (3/2)t2 + 3t + 1
Threfore
aT =
[(9/2)t3 + 7t + 2]/√[-(9/4)t4 + 7t2] + 4t + 5]
aN =
[- (3/2)t2 + 3t + 1]√[-(9/4)t4 + 7t2] + 4t + 5]
|
|