Complex integration
Contents
Residue calculus
© The scientific sentence. 2010
|
|
Complex integration :
Definitions
Definitions
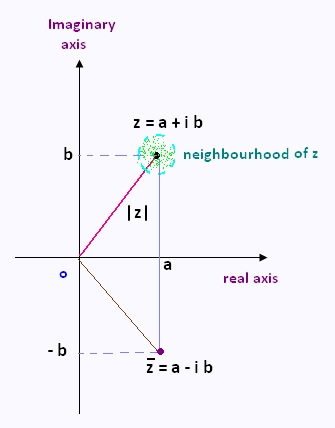
• A neighbourhood of a
point zo in the complex plane, is any open set containing zo.
• A function f of a complex variable z is continuous at zo if f(z) tends to f(zo) as z approaches zo.
• A function f of a complex variable z is differentiable at zo if
its derivative f'(zo) is well-defined (exists) at the point zo.
• Here is the definition of the derivative of f at zo:
• A function f is analytic in a neighbourhood U of zo if it is
differentiable everywhere in U. A function is entire if it is analytic
in the whole complex plane. We use also the terms regular and holomorphic as synonyms for analytic.
• A point zo is a singularity for a function f(z), if f is not analytic at zo.
• A point zo is an isolated singularity for a function f(z), if f is analytic in some disk around the singularity; that is, in 0 ≤ |z - zo| ≤ R. R is the radius of the disk.
The singularities of a rational function are always isolated.
• A point zo is a zero of f if f(zo) = 0.
• A point zo is a zero of order m of f if
f(zo) =
f'(zo) = f''(zo) = f(3)(zo) = ... f(m - 1)(zo) = 0; but
f(m)(zo) ≠ 0.
• The Laurent expansion of f around zo is
\[ \large\bf\color{teal}{
\textit f(\textit z) = \sum_{j = - \infty}^\infty
\textit a_j(\textit z - \textit z_o)^j}
\]
• The point zo is a removable singularity
of f, if the Laurent expansion
of f around zo has no negative powers; that is,
\[ \large\bf\color{brown}{
\textit f(\textit z) = \sum_{j = 0}^\infty
\textit a_j(\textit z - \textit z_o)^j}
\]
•
The point zo is a pole of order m for f, if the
Laurent expansion of f around zo starts from j = - m, so that
a- m ≠ 0. That is
\[ \large\bf\color{brown}{
\textit f(\textit z) = \sum_{j = - m}^\infty
\textit a_j(\textit z - \textit z_o)^j}
=
\\
\]
\[ \bf\color{indigo}{
\frac{a_{- m}}{(\textit z - \textit z_o)^m} +
... + a_0 + a_1(\textit z - \textit z_o) +
a_2(\textit z - \textit z_o)^2 + ...
\\
with \; a_{- m} \ne 0
}
\]
• A pole of order m = 1 is called a simple pole.
•
The point zo is an essential singularity of f if
f(z)(z - zo)n is not differentiable for any integer n > 0.
The Laurent series of f at the essential singular point zo has an infinite negative degree nonzero terms.
A singular point that is not a pole or removable singularity is an essential singular point.
Example: z = 0 is an essential singularity of f(z) = exp{1/z}.
|
|