Complex integration
Contents
Residue calculus
© The scientific sentence. 2010
|
|
Complex integration :
Residue theorem
1. Residue theorem : One pole zo
•
f(z) has a pole of order m at z = zo. The
Laurent expansion of f around zo starts from j = - m, so that
a- m ≠ 0. That is
\[ \large\bf\color{brown}{
\textit f(\textit z) = \sum_{j = - m}^\infty
\textit a_j(\textit z - \textit z_o)^j }
=
\\
\]
\[ \bf\color{indigo}{
\frac{a_{- m}}{(\textit z - \textit z_o)^m} +
... + a_0 + a_1(\textit z - \textit z_o) +
a_2(\textit z - \textit z_o)^2 + ...
\\
with \; a_{- m} \ne 0
}
\]
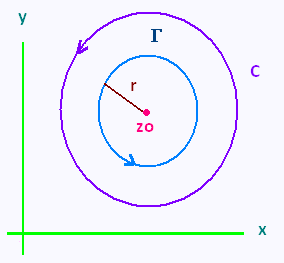
We want to ingegrate f(z) over a countour C. The circle C is centered at te point zo. Γ is the interior circle of radius r and centered also
on zo.
\[ \bf\color{brown}{
\oint_C f(z) dz = \oint_{\Gamma} f(z) dz
\\
Set z = zo + r exp{i\theta} \Rightarrow dz = i r exp {i\theta d\theta}
\\
\oint_C f(z) dz = \oint_C
\sum_{j = - m}^\infty
\textit a_j(\textit z - \textit z_o)^j
dz
=
\\
\sum_{j = - m}^\infty \textit a_j
\int_{0}^{2\pi}
(r exp{i\theta})^j
i r exp {i\theta} d\theta
=
\\
\sum_{j = - m}^\infty \textit a_j
\int_{0}^{2\pi}
i r^{j+1} exp{i (j + 1)\theta}
d\theta
}
\]
\[ \bf\color{black}{
\text {For j} \neq - 1,
\int_{0}^{2\pi}
i r^{j+1} exp {i (j + 1)\theta}
d\theta
=
\\
\frac {exp{i (j + 1)\theta}}{i(j + 1)}
|_0^{2\pi}
= 0
}
\]
\[\large\bf\color{red}{
j \neq - 1 \Rightarrow \oint_C f(z) dz = 0
}
\]
\[ \bf\color{black}{
\text {For j = - 1,}
\int_{0}^{2\pi}
i r^{j+1} exp{i (j + 1)\theta}
d\theta
=
\\
\int_{0}^{2\pi}
i d\theta
=
2\pi i
}
\]
\[\large\bf\color{red}{
j = - 1 \Rightarrow \oint_C f(z) dz = 2\pi i a_{-1}
}
\]
Therefore
\[\Large\bf\color{teal}{
\oint_C \textit f(\textit z) \textit d\textit z = 2\pi \textit i \textit a_{-1}
}
\]
2. Residue theorem
f(z) is continuous within and on a closed contour C; and
analytic, except for a finite number of poles
within C. The residue theorem or the Cauchy
Integral Formula reads:
\[\Large\bf\color{brown}{
\oint_C \textit f(\textit z) \textit d\textit z = 2\pi \textit i \sum_j \textit R_j
}
\]
\[ \bf\color{indigo}{
\sum_j R_j \; \text { is the sum of the residues of
}
\\
\text {the function f(z) at its poles within C.}
}
\]
|
|