Courbes
paramétrées
En coordonnées
cartésiennes
Exemples
En coordonnées
polaires
Exemples
© The scientific sentence. 2010

|
Mathématiques :
Courbes planes paramétrées
courbes paramétrées en coordonnées polaires
Plan d'étude d'une coube
paramétrée en coordonnées polaires
Les coordonnées polaires
Ici, on va étudier une courbe paramétrée en coordonnées
polaires:
θ  r(θ) r(θ)
définie sur un intervalle I de 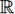
1. Ensemble de définition et d'étude
On réduit le domaine d'étude d'une courbe polaire par l'utilisation
de périodicité, parité ou autres symétries.
• Si f est T - périodique, il suffira d'étudier la fonction f sur
un intervalle d'amplitude T exemple : [-T/2 ; T/2[ , [0 ; T[ etc...
le reste de la courbe sera obtenue par rotations successives d'angle T.
• Si f est T - antipériodique, il suffira d'étudier la fonction f sur
un intervalle d'amplitude T exemple : [- T/2 ; T/2 [ , [0 ; T[ etc...
le reste de la courbe sera obtenue par rotations successives d'angle
T + π .
• Si f est paire , il suffira d'étudier la fonction f sur l'intervalle
[0 ; + ∞[ ou ] - ∞ ; 0] , le reste de la courbe sera
obtenue par symétrie axiale d'axe
l'axe des ordonnées .
• Si f est impaire , il suffira d'étudier la fonction f sur l'intervalle
[0 ; + ∞[ ou
] -∞ ; 0] , le reste de la courbe sera obtenue par symétrie axiale d'axe l'axe
des abscisses.
• Si il existe un réel a tel que pour tout réel θ de  ,
f (a - θ) = f (θ) , il suffira d'étudier la fonction f sur
l'intervalle [a/2 ; + ∞ [ ou
] - ∞ ; a/2] , le reste de la courbe sera obtenue par symétrie axiale
d'axe la droite d'équation polaire θ = a/2. ,
f (a - θ) = f (θ) , il suffira d'étudier la fonction f sur
l'intervalle [a/2 ; + ∞ [ ou
] - ∞ ; a/2] , le reste de la courbe sera obtenue par symétrie axiale
d'axe la droite d'équation polaire θ = a/2.
• Si il existe un réel a tel que pour tout réel θ de  ,
f (a - θ ) = - f ( θ ) , il suffira d'étudier la fonction f sur
l'intervalle [a/2 ; + ∞ [ ou ]- ∞ ; a/2] , le reste de la courbe
sera obtenue par symétrie axiale d'axe la droite d'équation polaire
θ = (a + π)/2. ,
f (a - θ ) = - f ( θ ) , il suffira d'étudier la fonction f sur
l'intervalle [a/2 ; + ∞ [ ou ]- ∞ ; a/2] , le reste de la courbe
sera obtenue par symétrie axiale d'axe la droite d'équation polaire
θ = (a + π)/2.
2. Branches infinies
Au voisinage de θo : si
r(θ)  ± ∞
lorsqueθ tend vers θo, alors
la courbe admet une branche
infinie de direction asymptotique la droite
d'angle polaire θ = θo. ± ∞
lorsqueθ tend vers θo, alors
la courbe admet une branche
infinie de direction asymptotique la droite
d'angle polaire θ = θo.
Pour étudier plus précisément cette branche infinie,
on utilise le repère (O,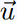 θo , θo ,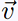 θo). θo).
Le point M(θ) de la courbe a pour coordonnées
dans ce repère
X(θ) = r(θ) cos(θ - θo) et
Y(θ) = r(θ) sin(θ - θo)
X(θ) tend vers ± ∞ lorsque θ tend vers
θo et la nature de la branche infinie est
donnée par le comportement de Y(θ) :
Si lim Y(θ) = l
θ  θo , θo ,
alors la courbe admet une asymptote d'équation = l
dans le repère (O,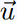 θo,
θo,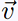 θo). θo).
Si lim Y(θ) = ± ∞
θ  θo , θo ,
alors la courbe admet une branche parabolique de
direction la droite d'angle polaire θ =
θo
Au voisinage de + ∞ : on distingue plusieurs
cas :
Si r(θ)  ± ∞ ,
, alors la courbe présente une branche infinie en forme
de spirale (qui s'écarte de plus en en plus de l'origine). ± ∞ ,
, alors la courbe présente une branche infinie en forme
de spirale (qui s'écarte de plus en en plus de l'origine).
Si r(θ)  a ≠ 0, alors la
courbe est une spirale qui s'enroule autour
du cercle de centre O et de rayon |a|, appelé cercle
asymptote de la courbe C. a ≠ 0, alors la
courbe est une spirale qui s'enroule autour
du cercle de centre O et de rayon |a|, appelé cercle
asymptote de la courbe C.
Si r(θ)  0,
alors la courbe se présente comme une spirale qui
s'enroule autour du point OO, qui est aussi appelé
point asymptote . 0,
alors la courbe se présente comme une spirale qui
s'enroule autour du point OO, qui est aussi appelé
point asymptote .
3. Etude locale d'un arc paramétré - tangente
Pour une courbe paramétrée en coordonnées polaires,
seule l'origine peut être un point stationnaire.
Ceci se produit si et seulement si r(θ) = 0
( à l'origine) et r'(θ) = 0 .
• Tangente ailleurs qu'en l'origine :
Soit Φ l'angle entre la tangente à la courbe en
θ et la droite (O,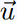 θ). Alors θ). Alors
tan Φ = r(θ)/r'(θ)
On a Φ = π/2 lorsque r'(θ) = 0
En particulier, en un point M(θ) de la courbe autre
que l'origine tel que r'(θ) = 0, la tangente à la
courbe en M(θ) est orthogonale à
la droite (OM(θ)).
• Tangente en l'origine :
si r(θ) = 0, la tangente à l'origine correspondante
est toujours dirigée par le vecteur 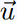 θ. θ.
|
|