Courbes
paramétrées
En coordonnées
cartésiennes
Exemples
En coordonnées
polaires
Exemples
© The scientific sentence. 2010

|
Mathématiques :
Courbes planes paramétrées
Position d’une courbe par
rapport à sa tangente
Position d’une courbe par rapport
à sa tangente
La tangente en M(to) à la courbe peut se
présenter de quatre façons :
• la courbe continue dans le même sens, sans traverser la tangente :
c’est un point d’allure ordinaire,
• la courbe continue dans le même sens, en traversant la tangente :
c’est un point d’inflexion,
• la courbe rebrousse chemin le long de cette tangente en la traversant,
c’est un point de rebroussement de première espèce,
• la courbe rebrousse chemin le long de cette tangente sans la traverser,
c’est un point de rebroussement de seconde espèce.
Pour déterminer de façon systématique la position de la courbe par
rapport à sa tangente en un point singulier M(t0),
on effectue un développement limité des coordonnées de M(t) =
(x(t), y(t)) au voisinage de t = to
. Pour simplifier l’expression on suppose to = 0. On écrit:
M(t) = M(0) + tp 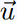 + tq
+ tq 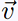 + tq
+ tq  (t) (t)
où :
• p < q sont des entiers,
• 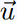 et et
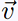 sont des vecteurs non colinéaires, sont des vecteurs non colinéaires,
•  est un vecteur, tel que est un vecteur, tel que
  (t) (t)
 0 lorsque t 0 lorsque t  to. to.
En un tel point M(0), la courbe C admet une tangente, dont un vecteur
directeur est 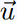 . .
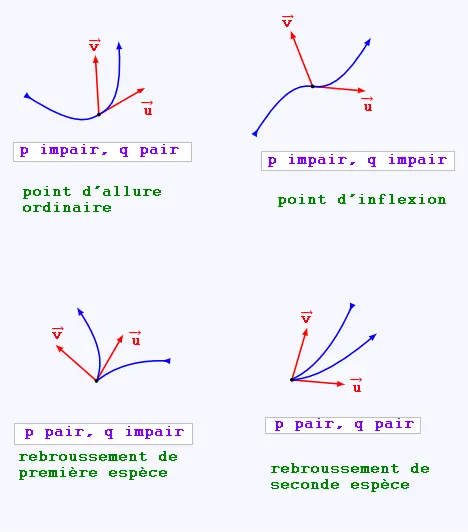
La position de la courbe C
par rapport à cette tangente est donnée par la parité de p et q :
|
|