Courbes
paramétrées
En coordonnées
cartésiennes
Exemples
En coordonnées
polaires
Exemples
© The scientific sentence. 2010

|
Mathématiques :
Courbes planes paramétrées
Courbe paramétrée: exemple 3
Courbe paramétrée: exemple 3
On veut étudier la courbe paramétrée par:
x(t) = t3/(t2 - 1)
y(t) = 1/(t3 - t)
• Domaine de définition :
La fonction x est définie sur  \ {- 1, 1} et y sur
\ {- 1, 1} et y sur  \ {- 1, 0, 1}. \ {- 1, 0, 1}.
On a donc Dom =  \ {- 1, 0, 1}. \ {- 1, 0, 1}.
• Réduction du domaine d’étude :
On a pour tout x de Dom la symétrie S1 suivante:
x(-t) = - x(t) et
y(-t) = - y(t)
La courbe est symétrique par rapport à O.
On l’étudie sur I = ]0, + ∞[ et on complètera
par la symétrie S1 par rapport à O.
Nous avons aussi la symetrie S2 suivante:
x(1/t) = - y(t) et
y(1/t) = - x(t),
La courbe est donc symétrique par rapport à
la deuxième bissectrice (droite y = - x).
On l’étudie sur I2 = ]0, 1[ et on complè-
tera par la symétrie par rapport à cette droite.
• Dérivées:
x'(t) = t2(t2 - 3)/
(t2 - 1)2
y'(t) = (3t2 - 1)/(t3 - t)2
Dans I2, la dérivée x'(t) est toujours négative
et y'(t) s’annule pour t = 1/√3. On a alors
x(t) = - √3/6 ≈ - 0.3 et
y(t) = - 3√3/2 ≈ - 2.6
• Asymptotes:
• Lorsque t tend vers 0, l’abscisse x(t) tend
vers 0, et l’ordonnée y(t) vers -8. La courbe
possède l’axe Oy comme asymptote verticale
lorsque t tend vers zéro.
• Lorsque t tend vers 1, on a:
y(t)/x(t) = 1/t4
Cette quantité tend vers 1.
Ensuite
y(t) - x(t) = - (t2 + 1)/t
tend vers -2. La courbe admet donc comme
asymptote obliqu la droite d’équation
y = x - 2 .
Pour étudier la position de la courbe par rapport
à cette asymptote, on étudie le signe de y(t) - y.
C'est à dire:
y(t) - x(t) + 2 = - (t - 1)2/t
Cette expression est négative sur I2. La courbe est en
dessous de l’asymptote.
Par symétrie, il existe une autre asymptote d’équation
y = x + 2 .
• Tableau de variation:
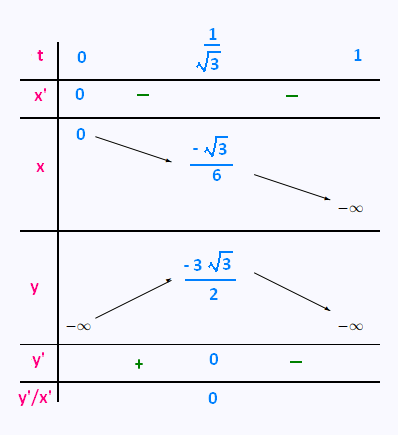
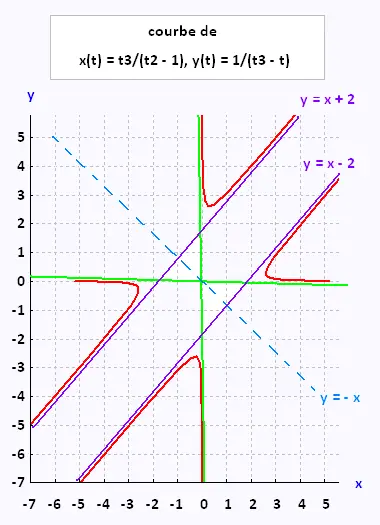
• Tracé de la courbe:
On trace l’arc de courbe obtenu lorsque t varie de
0 à 1, puis on complète par les deux symétries.
• Gnuplot code:
reset
set xtics 1
set ytics 1
set grid
set parametric
set isosamples 10,10
set xrange [-7:7]
set yrange [-7:7]
set ylabel "Y"
set xlabel "X"
set title " courbe de x(t) = t3/(t2 - 1),
y(t) = 1/(t3 - t)
plot t*t*t/(t*t - 1), 1/(t*t*t - t)
|
|