Mathématiques :
Courbes planes paramétrées
Courbe paramétrée: exemple 4

Courbe paramétrée: exemple 4

On veut étudier la courbe paramétrée par:

x(t) = t² + 2/t -3
y(t) = (1/3)(t² - 16/t)


• Domaine de définition :

Les fonctions x et y sont définies sur Dom = R*.

• Dérivées:

x'(t) = 2(t³ - 1)/t²
y'(t) = 2(t³ + 8)/3t²

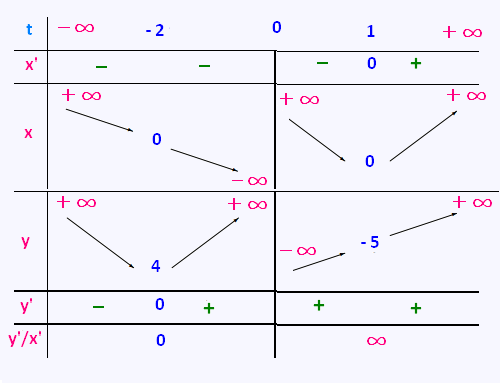
La fonction x' s’annule pour t = 1 et la fonction y' pour t = -2. La courbe admet une tangente horizontale en t = -2 et une tangente verticale en t = 1.

• Asymptotes:

• On étudie la courbe lorsque t tend vers 0.

On a alors

y(t)/x(t) = (t³ - 16)/3(t³ - 3t + 2)

Cette expression admet, en t = 0, pour limite a = - 8/3. Puis

y(t) - ax(t) = 3t² - 8,

admet pour limite b = - 8, ce qui montre que la courbe admet comme asymptote oblique la droite d’équation

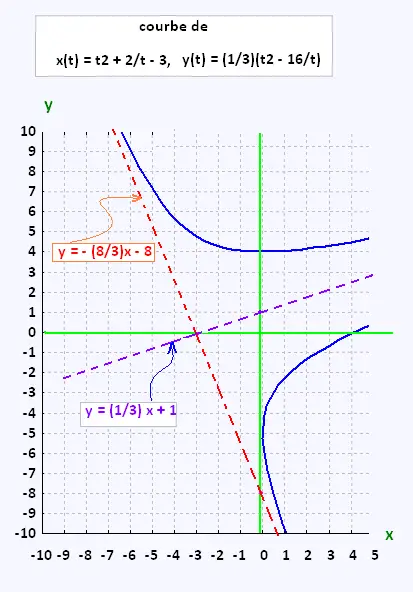
y = ax + b = - (8/3)x - 8.

La position de la courbe par rapport à cette asymptote est donnée par le signe de

y(t) - ax(t) - b = 3t².

La courbe est donc toujours au-dessus de l'asymptote.

• On étudie la courbe lorsque t tend vers l’infini.

On a encore

y(t)/x(t) = (t³ - 16)/3(t³ - 3t + 2)

et cette expression admet pour limite a' = 1/3 (la limite est le rapport des termes de plus hautdegré). Puis

y(t) - a'x(t) = (t - 6)/t admet pour limite b' = 1, ce qui montre que la courbe admet comme deuxième asymptote oblique la droite d’équation

y = a'x + b' = (1/3) x + 1

La position de la courbe par rapport à cette asymptote est donnée par le signe de

y(t) - a'x(t) - b' = - 6/t.

La courbe est donc au-dessus de l’asymtote si t < 0 et en dessous si t > 0.

• Tableau de variation:



• Tracé de la courbe:



• Gnuplot code:

reset 
set xtics 1
set ytics 1
set grid 
set parametric
set isosamples 10,10
set xrange [-10:5]
set yrange [-10:10] 
set ylabel "Y"
set xlabel "X" 
set title "  courbe de x(t) = t2 + 2/t - 3, 
y(t) = (1/3)(t2 - 16/t)"
plot t*t + 2/t - 3, (t*t - 16/t)/3