Mécanique:
Le mouvement circulaire
L'épicycloide

L'épicycloïde

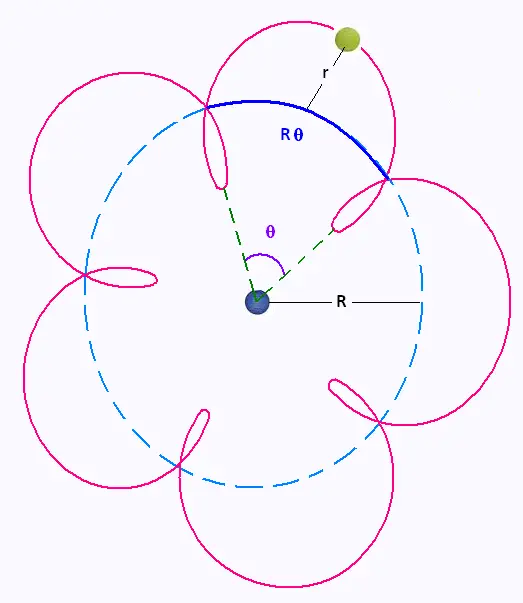
L' épicycloïde est la trajectoire d'un point sur un cercle en rotation à une vitesse constante dont le centre se déplace à vitesse constante sur la circonférence d’un autre cercle.

Une épicycloïde est formée d’arcs isométriques (appelés arches) séparés par des points de rebroussements.

On caractérise une épicycloïde par q le rapport simplifié du rayon du cercle de base R sur le cercle roulant r: q = R/r .

L'arc de cercle de base R θ est égal au tour complet du cercle roulant. Nous avons donc: R θ = 2 π r , soit: q = R/r = 2π/θ.

Soit a le nombre de rotations du cercle roulant nécessaires pour ramener le point mobile à sa position de départ (donc le nombre d’arches).

Soit b le nombre de fois que le cercle roulant fait de tours sur le cercle de base pour revenir au point de départ

Le rapport R/r doit remplir une autre condition: b 2π R = a 2π r, soit R/r = a/b .

En tout nous aurons: q = R/r = 2π/θ= a/b

q = R/r = 2π/θ = a/b

Les équations paramétriques d'une épicycloïde sont :

x(θ) = r[(q + 1) cos θ - cos((q + 1)θ)]
y(θ) = r[(q + 1) sin θ - sin((q + 1)θ)]