Courbes
paramétrées
En coordonnées
cartésiennes
Exemples
En coordonnées
polaires
Exemples
© The scientific sentence. 2010

|
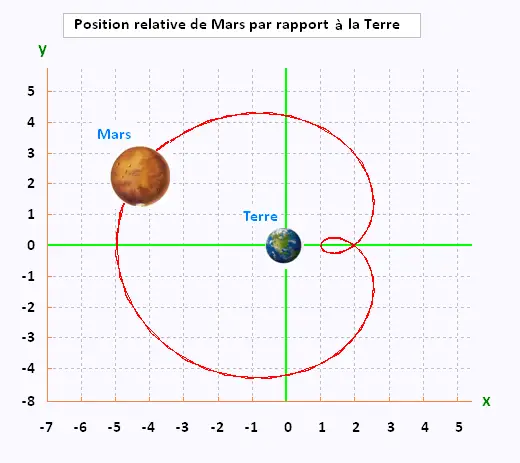
Le mouvement rétrograde de Mars
Mécanique:
Le mouvement circulaire
La cardioide
Le mouvement rétrograde de Mars
1. Le mouvement rétrograde de Mars
La rétrogradation ou mouvement rétrograde est le mouvement de recul.
Toutes les huit planètes du système solaire semblent décrire un
mouvement rétrograde.
Dans le système héliocentrique, c'est à dire où le Soleil est considéré
comme origine du repère, la trajectoire de la Terre est une ellipse, et celle
de Mars est aussi une ellipse.
Mais, dans le système géocentrique, c'est à dire où le Terre est considérée
comme origine du repère, la trajectoire de Mars est une cardiode.
Ce mouvement rétrograde apparent est de l'ordre de l'année ou plus. Il est dû aux mouvements des planètes autour du Soleil. C,est ce mouvement qui est à l'origine de l'apparition du phénomène de rétrogadation.
Un autre mouvement apparent des planètes et des astres est dû à la rotation de la Terre autour d'elle-même, qu'on appelle un mouvement diurne.
2. Équations paramétriques du mouvement
rétrograde de Mars par rapport au
référentiel géocentrique
Nous avons les données suivantes:
Terre:
Distance moyenne au Soleil = 1 ua
Période de révolution (en année terrestre) = 1
Excentricité (l'écart entre l'orbite et le cercle) = 0.017 ≈ 0
Inclinaison (par rapport à l'écliptique) = 0o
Mars:
Distance moyenne au Soleil = 1.5 ua
Période de révolution (en année terrestre) = 1.88 ≈ 2
Excentricité (l'écart entre l'orbite et le cercle) = 0.093 ≈ 0
Inclinaison (par rapport à l'écliptique) = 1o5, ≈ 0
• 1 ua (unité astronomique) = 1.5 x 1011 m
• L'écliptique est le cercle qui représente la trajectoire annuelle
apparente du Soleil vue de la Terre. Le plan écliptique est le plan contenant l'orbite de la Terre autour du Soleil.
Les excentricités des deux planètes sont faibles on peut donc considérer les deux trajectoires elliptiques par des cercles. Les inclinaisons sont petites, on peut donc considérer les deux trajectoires coplanaires dont le centre est le Soleil.
Pour représenter la trajectoire de Mars par rapport à la Terre, nous aurons donc
besoin seulement des deux données suivantes:
|
Rayon du cercle
(en demi ua) |
Période de
révolution
(en années terrestres) |
| Terre |
2 |
1 |
| Mars |
3 |
2 |
En notation comlexe les positions respectives Z(T,S) et Z(M,S) de la Terre et de Mars , mesurées en demi unité astronomique, par rapport au Soleil seront
paramétrisées en fonction du temps t (mesuré en année terrestre):
Z(T,S)(t) = 2 exp{2π i t}
Z(M,S)(t) = 3 exp{π i t}
La position relative de Mars par rapport à la Terre est :
Z(M,T)(t) = Z(M,S)(t) - Z(T,S)(t) = 3 exp{π i t} - exp{2π i t}
En utilisant la propiété d'Euler, exp{ix} = cos x + i sin x, puis en
séparant la partie réelle (abscisse) de la parie imaginaire (ordonnée),
on obtient les équations paramétriques d'une cardioïde:
x = 3cos(πt) - 2cos(2πt),
y = 3sin(πt) - 2sin(2πt)
|
|