Courbes
paramétrées
En coordonnées
cartésiennes
Exemples
En coordonnées
polaires
Exemples
© The scientific sentence. 2010

|
Mathématiques :
Courbes planes paramétrées
Courbe paramétréeen polaire
La rosace à huit feuilles
La rosace à huit feuilles
On considère la courbe définie par son équation polaire :
r(θ) = sin (4θ)
Nous avons:
r(θ + π/2) = r(θ)
La fonction polaire r(θ) est (π/2)-périodique.
on peut donc tracer la courbe sur un intervalle de
longueur π/2, puis de compléter en utilisant les 3
rotations de centre O et d'angle π/2, π et 3π/2.
On se limite à l'intervalle [-π/4, π/4].
On remarque ensuite que :
r(- θ) = - r(θ).
On peut donc se
contenter de tracer la courbe sur l'intervalle [0,π/4, et
on complètera le tracé par une symétrie d'axe (Oy).
Enfin, on :
r(π/4 - θ) = r(θ).
On va donc tracer la courbe sur l'intervalle
[0, π/8] , et on va compléter le
tracé par une symétrie d'axe polaire d'angle π/8.
Sur [0, π/8], la fonction r(θ) est croissante,
valant 0 en 0 et 1 en π/8.
Le point correspondant à θ = 0 est un point stationnaire, la
tangente à ce point est dirigée par le vecteur 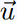 o ,
c'est-à-dire que la tangente en ce point est l'axe des abscisses. o ,
c'est-à-dire que la tangente en ce point est l'axe des abscisses.
En π/8, r'(θ) = dr(θ)/dθ s'annule, et donc la tangente est
perpendiculaire au rayon vecteur, ie à 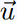 π/8. π/8.
Finalement, on obtient le tracé suivant :
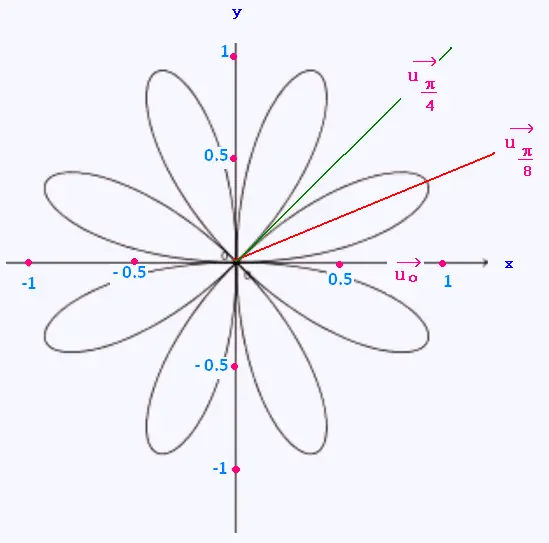
|
|