Applications of Ampere's law
Ampere's law is used to determine the magnetic field produced by
a current distribution with a symmetry, exactly as the Gauss's law
is used to determine the electric field produced by
a charge distribution with a symmetry. Note that the Gauss's
law involves a surface integral of an electric field, whereas
Ampere's law involves a line integral to determine a magnetic
field.
1. Long straight wire carrying a current I
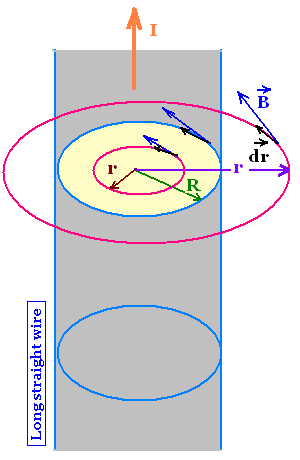
We want to determine the magnetic field B due to
a long straight wire of radius R and current density J;
carrying a current I inside the wire (r<R) at the
edge of the wire (r = R) and outside the wire (r>R).
The current crossing the wire is I piercing the surface πR2.
The current that pierces the surface πr2 is
πr2 (I/πR2) = (r2/R2) I.
1.1. r < R:
Ampere's law gives:
∮ B dr = μo (r2/R2) I
∮ B dr = 2πr B. Therefore:
2πr B = μo (r2/R2) I
B = (μoI/2π) (r/R2)
B = (μoI/2πR2) r
1.2. r = R:
Ampere's law gives:
∮ B dr = μo (R2/R2) I
∮ B dr = 2πR B. Therefore:
2πR B = μo I
B = μoI/2πR
B = μoI/2πR
1.3. r > R:
Ampere's law gives:
∮ B dr = μo I
∮ B dr = 2πr B. Therefore:
2πr B = μo I
B = (μo/2π) 1/r
B = (μo/2π) 1/r
1.4. Graph of B(r)
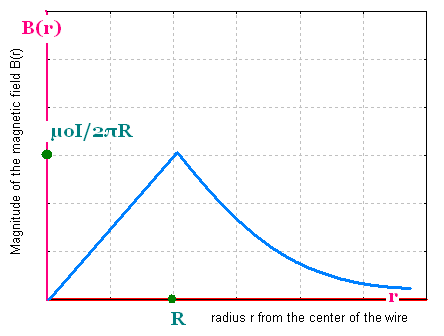
The magnitude of the field increases linearly with distance R from
the axis inside the wire. Outside the wire the magnitude of the field
decreases inversely with the distance r.
2. Ideal solenoid
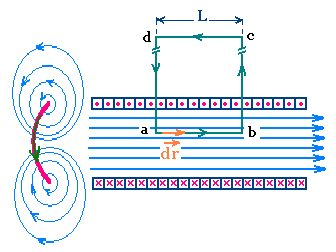
A solenoid is formed by winding a long wire onto
a cylinder. We are interested to determine the magnetic field produced
a solenoid carrying a current, with n the number of turns
per unit length (turns/meter).
∮ B dr = ∮(ab) B dr +
∮ B(bc)dr +
∮(cd)B dr +
∮(da)Bdr = μo Σi
Because dr is perpendicular to B:
∮ B(bc) dr = 0
We can chose (bc) and (da) as long as possible (infinity)
and have B there = 0:
∮(cd)Bdr = 0
Because dr is perpendicular to B:
∮(da)Bdr = 0
Only the nonzero part ∮(ab)Bdr
contributes to the magnetic field.
∮Bdr = ∮(ab)Bdr = B L
If N is the number of turns within the length L then Σi = NI.
N is also equal to nL. Hence Σi = nLI
Ampere's law gives:
∮Bdr = μoΣi, that is
B L = μo n L I
We obtain then
B = μonI
Magnetic field of an ideal solenoid currying a current I
with n turns per unit length. Magnetic field outside is 0 and
inside uniform and parallel to the axis:
B = μonI
3. Force between currents
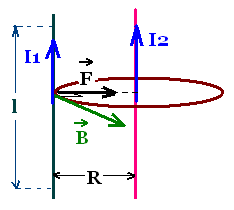
Consider two parallel long straight wires carrying the currents
I1 and I2 separated by a distance R.
The current I2 produces the magnetic field B
where the first wire is located.
B is tangent to the circle and perpendicular to the segment l that
we consider on the first wire. Amper's law gives:
B2 = μoI2/2πR
The magnetic force due to B and I1 is :
F = B2I1l =
μoI2 I1l/2πR
Force between currents:
F = μoI2 I1 l/2πR
|