Faraday's law
From Gauss's law for a magnetic field, the closed surface
integral of B is zero, that is the flux of B piercing a closed
surface is zero. In this section, we are considering
the flux of a magnetic field piercing an open surface.
1. Magnetic flux for an open surface
bounded by a conducting loop
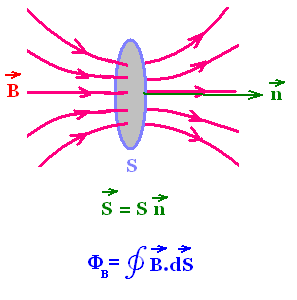The flux of the magnetic field B through the open surface S with
a normal vector n, is the dot product of the vectors B and S.
If the vector magnetic field B is taken perpendicular to the
surface S (cosθ = 1), the flux is simply equal to the product BS.
→ →
ΦB = ∮ B . dS
2. Magnetic Induction
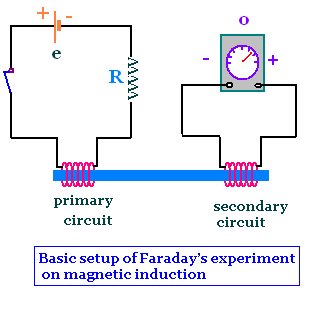
Since a steady current in a wire produces a steady magnetic field,
Faraday thought at first that a steady magnetic field could
produce a current.
His investigations by experiments
showed that the occurred only when
the current is varying.
magnetic induction
A current in the primary circuit produces a magnetic field
which is concentrated in the iron bar. The secondary circuit is
connected to the galvanometer that indicates the presence of
any induced current in that circuit.
When the position of the switch on the primary
circuit is changed from open to closed, a current is detected
in the galvanometer. When the position of the switch is changed from closed to
open the induced current with the opposite sense appears in the galvanometer.
If the current in the primary circuit does not change,
no induced current appears in the secondary circuit. Hence there
is no induced current for a steady magnetic field.
Thus the induced current exists only when the
magnetic field, due to the current in the primary circuit,
is changing.
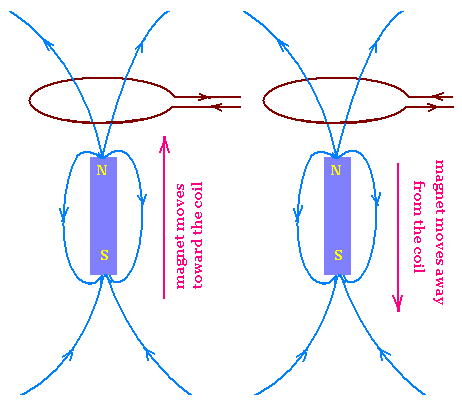
Changing a magnetic field, like in the circuit, can be also
done by moving a magnet inside a coil or the inverse, that is
moving a coil through a magnet. If the magnet is at rest
relative to the coil, then no induced current exists. But if the
magnet is moved toward the coil or the coil moved toward the
magnet, then a current is induced. If the
magnet is moved away from the coil or the coil moved away from the
magnet, then a current is induced with the opposite sense.
Further, changing the shape of the coil or a loop relative
to a magnetic field produces also an induced current in the galvanometer.
Therefore, a change in the magnetic field B, or a change in the
surface pierced by B, or a change in the direction between the two
vectors B and S give rise to an induced current. In sum, a change in the
flux of B through the surface S bounded by conductor will induce a current
in this conductor.
3. Faraday's law
The presence of such currents in the secondary circuit implies the existence
of an induced emf ℰ; that is an energy supplied to the
charge carriers to traverse the circuit.
Hence the change in the flux of the magnetic flux B linking a
loop (conductor) gives rise to an emf ℰ in this loop. The change in
the flux and the emf are related by Faraday's law:
ℰ = - dΦB/dt
Faraday's law:
ℰ = - dΦB/dt
The negative sign in this formula relates to the sense of the induced
emf in the circuit. This sign is determined by Lenz's law:
The sense of the induced current is such that its contribution
to magnetic field opposes the change in magnetic field which produces this
induced current.
The dimension of the emf ℰ is the V (Volt = Weber/second).
If we consider a closely wound coil with n turns, each turn in
the coil behaves as a loop. In each loop is induced an emf
e = - dΦB/dt. The total emf (in V) in the coil is the sum
of the emfs in each turn:
Emf of coil with n turns:
ℰ = - n dΦB/dt
Notice that the induced current in the loop or coil produces its own magnetic
field that to add to the inductor magnetic field. We can neglect the
induced magnetic field by assuming the resistor in the secondary
circuit is large so that the induced current is small.
|
