RC circuits

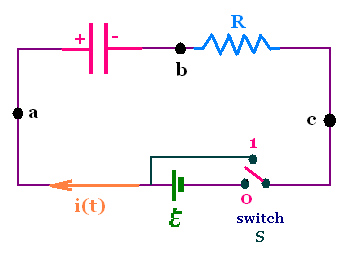
A capacitor is a device which can hold or contain charge on its plates, charge +Q on one plate and - Q on the other. The potential difference across a charged capacitor is V = Q/C, where C is the capacitance of the capacitor.

We examine two specific cases:
- Charging a capacitor: Switch on the position 0, and
- Discharging a capacitor: Switch on the position 1.

The circuit that contains a resistor and a capacitor is called an RC circuit. Its main characteristic is the variation with respect to time of the electric current across the circuit.

1. Charging a capacitor

1.1. Charge and current

At the time the switch is closed, the battery begins transferring charge carriers from one capacitor plate to the other; and the current starts to circulate across the circuit.



Beginning at the point c, the sense of the current is clockwise, Kirchhoff's loop rule gives:

(V_a - V_c) + (V_b - V_a) + (V_c - V_b) = 0

That is:

+ ℰ - (Q/C) - R I = 0

Q is the instantaneous charge on the positive plate of the capacitor. Since I = dQ/dt, the rate at which the capacitor is charging, we find:

ℰ = (Q/C) + R I = Q/C + R(dQ/dt)

dQ/dt = ℰ/R - Q/RC

dQ/(ℰ/R - Q/RC) = dt     (Eq.1)

Let: ℰ/R - Q/RC = z , so dz = - dQ/RC

The equation (Eq.1) becomes:

- RC dz/z = dt thus dz/z = - dt/RC

Integrating gives:

z = const . exp{- t/RC}

At t = 0, Q = 0, hence z = ℰ/R

Therefore

z = ℰ/R exp{- t/RC}

That is

ℰ/R - Q/RC = ℰ/R exp{- t/RC}

Rearranging, we find:

ℰ - ℰ exp{- t/RC} = Q/C

Solving for Q gives:

Q = ℰC[1 - exp{- t/RC}]



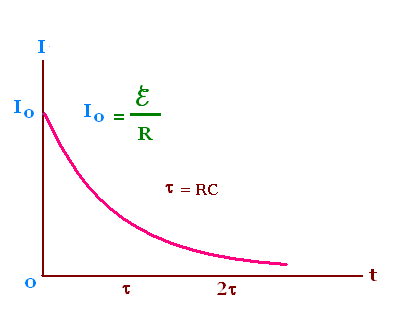
Taking the time derivative of the equation of Q gives:

I = dQ/dt = (ℰ/R)exp{- t/RC}

Let the initial current I_o = ℰ/R, and τ = RC the time constant. Hence

I = I_o exp{- t/RC}

Notice that the current I_o is the steady current that would exist in the capacitor is replaced by a connecting wire.

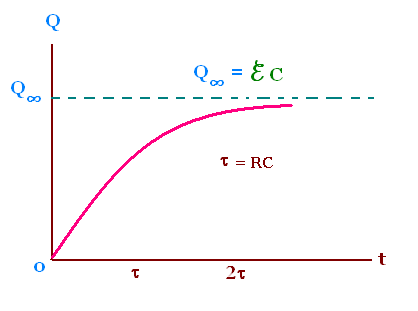
As time goes on, t tends to ∞ the final charge on the capacitor is Q_∞ = ℰC.

The product τ = RC represents the rate at which the capacitor is charged. This product of dimension time is called time constant of the circuit.

1.2. Energy exchanged in the circuit

During the charging process of the capacitor, energy is transferred by the emf ℰ of the battery to the charges carriers of the circuit.

During the entire charging process of the capacitor as t tends to ∞, the entire charge is Q_∞.

The energy by unit charge transferred by the battery is equal to its emf ℰ. During the entire charging process the charge that passes through the battery is Q_∞. Hence, the energy transferred by the battery, during the entire process of charging the capacitor, is:

ℰQ_∞ = ℰℰC = ℰ²C.

Since the energy stored in the capacitor with the charge Q is (1/2)Q²/C ; the energy stored in the capacitor after the charging process is completed is: E_capacitor = (1/2)Q_∞²/C = (1/2)(ℰC)²/C = (1/2) C ℰ².

E_capacitor = Cℰ²/2

Thus half of the energy expended by the emf of the battery is stored in the capacitor.

The other half of this energy is dissipated as heat in the resistor. The rate at which energy is dissipated in the resistor is P = - dU/dt = RI², where U is the electric potential energy of the carriers.

During the charging of the capacitor, the energy dissipated is E_heat = - ΔU = - ∫dU = ∫RI²dt (from 0 to ∞) =
∫R I_o² exp{- 2t/τ} dt = R I_o² ∫exp{- 2t/τ} dt.

Let x = 2t/τ thus dx = 2/τ dt ∫ exp{- 2t/τ} dt = (τ/2)∫exp{- x} = - (τ/2) exp{- x} (from 0 to ∞) = (τ/2) . 1 = τ/2.

Therefore

E_heat = - ΔU = R I_o² . τ/2 = R (ℰ/R)² . RC/2 = (ℰ)² . C/2

E_heat = Cℰ²/2

2. Discharging a capacitor

Initially the capacitor is under the potential difference V_o, and has the charge Q_o. The time we disconnect it from the battery, the charge carriers begin to flow through the circuit to discharge the capacitor. The flow of these carriers constitutes a current in the circuit.

Let Q(t) be the charge on the capacitor at time t. The sense of the current is counterclockwise, Kirchhoff's loop rule gives:

(V_a - V_b) + (V_c - V_a) + (V_b - V_c) = 0

That is

Q/C - R I = 0

Since I is positive and dq/dt is negative, because the charge on the plates is decreasing, I = - dQ/dt. Rearranging, we have:

dQ/Q = - dt/RC

The indefinite integral gives:

Q(t) = const exp {- t/RC}

With Q(0) = Q_o, we have const = Q_o, hence

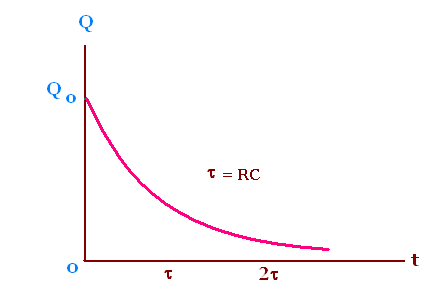
Q(t) = Q_o exp {- t/RC}

Q(t) = Q_o exp {- t/RC}



Taking the time derivative of the equation of Q gives:

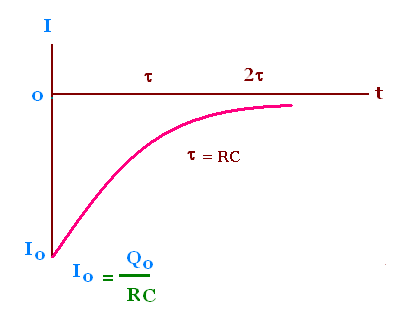
I = - dQ/dt = (Q_o/RC) exp {- t/RC}

Let the initial current I_o = Q_o/RC = V_o/R, and τ = RC the time constant that characterize the decay of the current. Hence

I = I_o exp{- t/RC}