|
Electrostatics
Electromagnetics
Electricity &
Magnetism
© The scientific sentence. 2010
|
Series RLC circuits
Capacitors and inductors are energy-storage devices. A capacitor
stores electric energy and an inductor stores magnetic energy.
Resistors just cause energy to be dissipated as a heat.
1. LC circuit: Oscillations
we examine the behavior a real circuit (resistance is significant), which
contains an inductance L, a capacitance C, and a resistor R,
an RLC circuit.
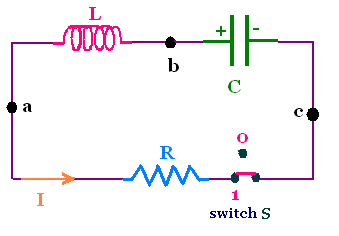
The capacitor in the circuit is charged by an
external battery and then the battery is taken away.
When the switch is closed (position 1), the capacitor will
begin to discharge through the inductor and the resistor.
During the discharging, there is a current I(t) crossing the
circuit and charge Q(t) on the plates of the capacitor.
The current I is the rate at which charge is transferred from
a plate to the other. In the figure, the sense of the current
(positive) is counterclockwise.
The potential difference between the plates is positive.
The potential through the inductor decreases then the difference
between the terminals of the inductor is negative.
The potential difference between the terminals
of the resistor is negative.
Kirchhoff's loop rule gives:
(Vb - Vc) + (Va - Vb) +
(Vc - Va) = 0
.
That is
+ Q/C - L (dI/dt) - R I = 0 (Eq. 1)
We have I = ± dQ/dt
During the discharging of the capacitor, Q decreases,
hence dQ is negative so is I = dQ/dt and d(dQ/dt)/dt =
d2Q/dt2.
Therefore
I = - dQ/dt. The equation (Eq. 1) becomes:
Q/C + L d2Q/dt2 + R I = 0
.
Rearranging, we find
d2Q/dt2 + (1/LC)Q + (R/L) dQ/dt = 0
Equation of RLC oscillation circuit:
d2Q/dt2 + (R/L) dQ/dt + (1/LC)Q = 0
2. Expression of the charge Q(t)
This differential equation is the same as the
differential equation of a damped harmonic oscillator,
like the mass-spring with friction system. The mass-spring-friction
harmonic oscillator provides a mechanical analog to the RLC circuit
Using the solutions of a
second
order differential equations, we have:
a) Δ = (R/L)2 - 4/LC > 0:
Q(t) = C1 exp{r1t} + C2 exp{r2t}
With
r1 = (- R/L + Δ1/2)/2
r2 = (- R/L - Δ1/2)/2
b) Δ = (R/L)2 - 4/LC = 0:
Q(t) = = C1 exp{r t} + C2 t exp{r t}
With
r = - R/2L
c) Δ = (R/L)2 - 4/LC < 0:
Q(t)= C1 exp{r1t} + C2 exp{r2t} =
exp{αt} (c1 cos βt + c2 sin βt)
With
α = - R/2L
β = (- Δ)1/2/2
The electromagnetic energy of an LC circuit is constant because
its resistance is negligible. The electromagnetic energy of the
RLC circuit is not constant. It decreases with time because energy is
dissipated as heat from the resistor.
Among the three cases given by the value of Δ the real
solution is the third case in which Δ < 0. In an
RLC circuit, the charge on the capacitor and the current in the
circuit will tend to approach zero as time goes by, and the
oscillations in the charge and current my occur while they
are dying out.
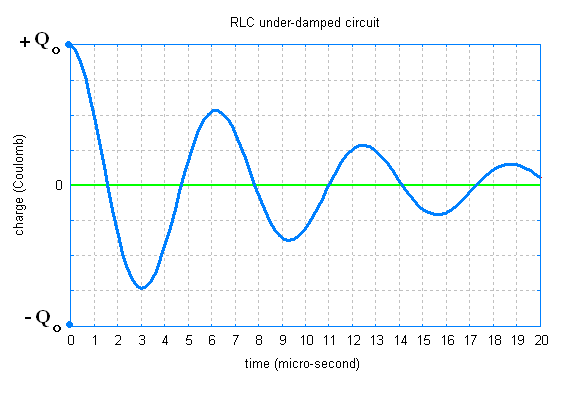
RLC under-damped circuit: Oscillating charge with damping
ωo = [(1/LC)]1/2, τ = 2L/R,
damped angular frequency:
ωd = [(1/LC) - (R/2L)2]1/2 =
[ωo2 - (1/τ)2]1/2
Q(t) = Qm exp{- t/τ} cos (ωdt + φ)
If R > (4L/C)1/2, the circuit is over-damped
If R = (4L/C)1/2, the circuit is critically over-damped
If R < (4L/C)1/2, the circuit is under-damped
3. Example
R = 200.00 Ω , L = 1.00 mH, and C = 1.00 nF
4L/C = 4 x - 3 / 10- 9 = 4 x 106
(4L/C)1/2 = 2 x 103
200 < 2000, hence
R < (4L/C)1/2, the circuit is under-damped
τ = 2L/R = 2 x 10- 3/200 = 10- 5 /second
R/2L = 1/τ = 105 second
1/LC = 1/1 x 10- 3 x 10- 9 = 1012
ωo = [(1/LC)]1/2 = 106
ωd = [(1/LC) - (R/2L)2]1/2 =
[1012 - 1010 ]1/2 =
105 [99]1/2 ≈ 106/second
For the initial conditions such that
Qm = Qo,
and φ = 0, we have:
Q(t) = Qo exp{- 105 t} cos (106t )
Q(t µs) = Qo exp{- t/10} cos(t)
|
|