Capacitors & insulators

1.Capacitor and capacitance

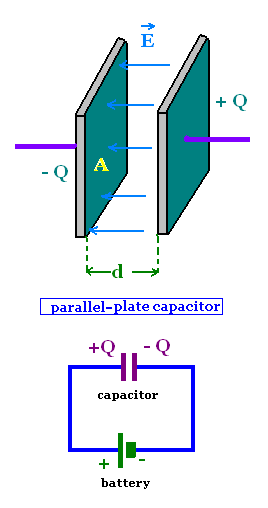
A capacitor is a device used in electric circuits. Its main importance is the temporary storage of energy in circuits. The capacitance is the ability of the capacitor to store energy.

A capacitor consists of two nearby conductors referred to plates separated from one another by an insulator, called dielectric.

A capacitor can be charged by connecting its two wires from the plates to the terminals of a battery. The battery pumps or moves electrons from a plate to the other. Thus the first plate becomes positively charged and the second becomes negatively charged. The circulation of the electrons through the circuit cease to flow at a certain time, the capacitor becomes charged, therefore the circuit is in equilibrium and the potential difference between the two plates of the capacitor and between the terminals of the battery become equal: ΔV(Capacitor) = ΔV(Battery), or simply V(C) = V(B), that is the voltages are the same. The potential difference on the battery is the potential difference across the capacitor.

At the equilibrium, the plates become charged with the charge +Q and -Q. The plate with +Q is the positive charged plate connected to the terminal + of the battery. The plate with -Q is the negative charged plate connected to the terminal - of the battery.

Thus the two plates posses equal but opposite charge and the net charge on the capacitor is zero. The charge Q on a capacitor refers to the magnitude of the charge on each plate.

Experiments show that the more the potential difference V across the capacitor is large, the more the charge Q on the capacitor is large, and the relationship between V and Q is proportional Q = C V.

The ratio C = Q/V is characteristic of a given capacitor. This ration is called capacitance C of the capacitor.

The capacitance is the measure of the ability of the capacitor to hold charges on it. The SI unit of capacitance is Coulombs/Volts (C/V), called a Farad (F). 1 F = 1 C/V.

The Farad is a large unit of capacitance. Typically, in electric circuits, the capacitance of capacitors ranges from 10^-12 F or 1 pF (picofarad) to 10^-6 F or 1 µF (microfarad)

2. Capacitance of parallel-plate capacitor

We have seen the potential difference across the parallel-plate capacitor is V = E d , and E = σ/ε_o, with σ = Q/A.

Therefore

V = E d = Q/C . Hence

C = Q/Ed = (σ A)/(σ/ε_o)d = A ε_o/d

A is the area of the plate and d is the plate separation of the capacitor. ε_o is the permittivity of free space (or vacuum), that is the medium between the two plates.

3. Capacitance of cylindrical capacitor

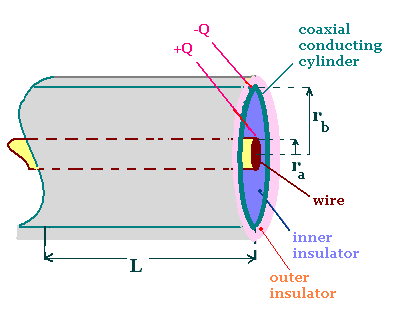
We treat the wire as the positive plate and the cylinder as the negative plate.

We have seen the field near a long line charge is E (r) = λ/2πε_or, with λ = Q/L, and r is the distance from the wire to a point outside the wire.

The potential difference between the wire of radius r_a and the cylinder of radius r_b is:

	rb
Vb - Va = - ∫	E	dr
	ra

Or

	rb
V = Va - Vb = ∫	E	dr
	ra

=

	rb
λ/2πεo ∫	(dr/r)	= (λ/2πεo) ln(rb/ra) = (Q/2πεoL) ln(rb/ra)
	ra

Therefore

C = Q/V = (2πε_oL) / ln(r_b/r_a)

4. Combination of capacitors

As cirduit elements, capacitors can be connected in series or in parallel.

4.1. Capacitors connected in series

Consider two capacitors of capacitance C1 and C2 connected in series.

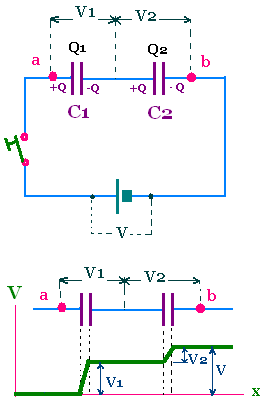Under electrostatic conditions, the potential is uniform along the connecting wires. The potential varies from the point a to the point b. The potential difference across both V = V_b - V_a is equal to the sum of the potential difference across each capacitor V = V₁ + V₂.

The two capacitors are initially uncharged, thus the region between them has a zero net charge, thus the two capacitors have the same charge Q = Q₁ = Q₂.

Now, we are interested to find the equivalent capacitance C12 fo the series combination of capacitors 1 and 2.

The equivalent capacitance of a combination of capacitors is the capacitance of a single capacitor wich, when used in place of the combination, provides the same external effect as the replaced capacitors. For the capacitors in series, this single capacitor must have the same charge Q under the same potential difference V. That is

If C1 = Q/V1 and C2 = Q/V2, Using V = V1 + V2, we have then:

V = V1 + V2 = Q/C1 + Q/C2 = Q(1/C1 + 1/C2) = Q/C12

Therefore

1/C12 = 1/C1 + 1/C2

Generally, the equivalent capacitance C_eq of a combination of many capacitors in series is such that:

1/C_eq = Σ (1/C_i). Where C_i is the individual capacitance.

4.2. Capacitors connected in parallel

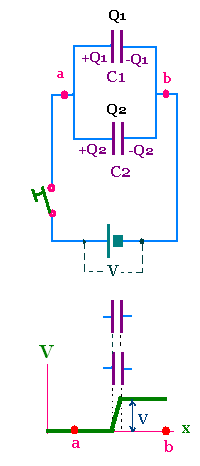
Let two capacitors of capacitances C1 and C2 connected in parallel. To provide the same external effect as capacitors 1 and 2 in parallel, a single capacitor with capacitance C12 , which will replace them, must have charge Q = Q1 + Q2 under the potential difference V. That is

C12 V = C1 V + C2 V = (C1 + C2) V

Therefore

C12 = C1 + C2

In general, the equivalent capacitance C_eq of many capacitors connected in parallel is:

C_eq = ΣC_i

5. Electric energy

5.1. Electric energy stored in a capacitor

When a battery charges a capacitor, the battery does work on the charges carriers, as it transfers them from the plate to the other, raising their potential energy. This is the electric energy stored in the capacitor.

Let U represent the energy of the capacitor after it has been charged to the final charge Q and final potential difference V, Q' and V' represent these quantities as they vary during the charging process.

During the charging process Q' varies while the battery transfers charge from a plate to the other, hence V' varies.

The potential V is the potential energy U per unit charge dQ.
At some instant during the charging process, the change in the potential energyis dU' = V'dQ'

Using V' = Q'/C , where C is the capacitance of the capacitor, we write:

dU' = V'dQ' = (Q'/C) dQ'

To find the potential energy U in the capacitor after being charged, we integrate dU':

	Q
U = ∫		(Q'/C) dQ = (1/2C) Q2
	0

5.2. Energy density of an electric field

We have associated the energy of the capacitor with the potential energy of the charges. This energy can be attributed to the electric field that exists between the plates.

We take the case of the parallel-plate capacitor in which the capacitance is C = A ε_o/d, and V = E d, we obtain:

U = CV²/2 = A ε_oV²/2d = ε_oE²(Ad)/2

The factor (Ad) is the volume of vacuum between the plates occupied by the electric field E. Therefore, the energy density, that is the energy per unit volume is u = U/(Ad) = ε_oE²/2

Hence

The energy density between two acculations of charge distribution separated by vacuum is

u = ε_oE²/2