|
Electrostatics
Electromagnetics
Electricity &
Magnetism
© The scientific sentence. 2010
|
Electrostatics: Electric field
Continuous charge distributions
1. Electric field due to
continuous charge distributions
A macroscopic objects such as rings, rods,
disks, or spheres are charged when they
have an imbalance of electrons and protons
populations. The charge of such an object is
treated as continuous distribution of
elementary charges dq.
The electric field due
to this charge dq is dE = k dq/r ^r where r
is the distance from the element of charge dq
to the point P where the electric field is evaluated, and
^r is the unit vector that points from dq to
the point P.
The electric field due to the whole
object at the point P is E = ∫ dE, or
2. Examples
2.1. Line charge
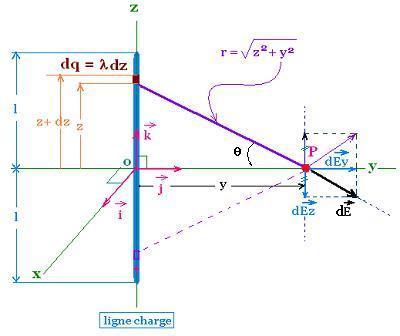
A line charge is a distribution of charge spread along
long and thin wire. A uniform line charge has a linear charge density λ that is equal to the charge Q of the whole line divided by its length l. λ = Q/l.
We want to find the expression of the electric field E in the perpendicular
bisector plane of a uniform line charge.
We have
λ = Q/l = dq/dz
The contribution of dq is dE = k dq/(z2 + y2).
The elementary field has two components:
dEy = dE cos θ
dEz = dE sin θ
cos θ = y/[y2 + z2]1/2
sin θ = z/[y2 + z2]1/2 =
Therefore
dEy = k dq/(z2 + y2)
y/[y2 + z2]1/2 =
k y dq/(y2 + z2)3/2 =
k y λ dz/(y2 + z2)3/2
dEz = k dq/(z2 + y2)
z/[y2 + z2]1/2 =
k z dq/(y2 + z2)3/2 =
k z λ dz/(y2 + z2)3/2
The contribution along the y-axis is:
E(y) = ∫ dEy
We have
For this result, go to
 ∫ dz/(y2 + z2)3/2 dz ∫ dz/(y2 + z2)3/2 dz
Replacing this result in the expresion of E(y),
we find:
E(y) = 2lkλy/y2[y2 + l2]1/2
E(y) = 2lkλ/y(y2 + l2)1/2
The contribution along the z-axis is:
E(z) = ∫ dEz
The function
f(z) = z /(z2 + y2)3/2 is an odd function, so
its definite integral between - l and + l is null. That is the
contribution of the upper half is cancelled by the contribution
of the lower half.
Finally the expression of the electric field E(y)
for a line charge of length l and linear charge density λ
at a point y in the perpendicular bisector plane is
2.2. circular ring
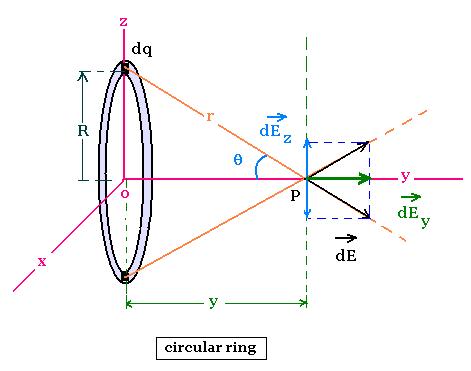
A circular ring contained in the plan
xz, centered at the origin, of charge Q, and
of radius R, is narrow enough to be considered as
circular line charge. As for the above example of
the line charge, by symmetry, only the y-components
contributes.
dE = k dq cos θ/r2
r2 = R2 + y2
r is constant for a fixed y.
The complete electric field E at the position
y due to the whole ring is:
E = ∫ dE = k cos θ/r2 ∫ dq =
k Q cos θ/r2
cos θ = y/r = y/(R2 + y2)1/2
Therefore
E(y) = k Q y/(R2 + y2)3/2
2.3. surface charge

The total charge of the disk is Q = 2πR2 σ.
σ is the surface charge density of the disk .
The elementary charge the related washer at the position
z is dq = σ 2π z dz . Therefore
The elementary electric field at the position y is
dE(y) = k dq cos θ/r2 =
k σ 2π z dz cos θ/r2 =
k σ 2π z dz y/(y2 + z2)3/2
Therefore
The total electric field at the point y due to the hole disk
is:
E(y) = ∫ dE
| |
+ R
| |
| E(y) = ∫ | |
k σ 2π z dz y/(y2 + z2)3/2
|
| |
0
| |
| |
+ R
| |
| = k σ 2π ∫ | |
z dz y/(y2 + z2)3/2
|
| |
0
| |
A primitive of z/(y2 + z2)3/2
is - 1/(y2 + z2)1/2
So
E(y) = k y σ 2π [1/(y2)1/2 - 1/(y2 + R2)1/2]
=
σ y /2εo [1/(y2)1/2 - 1/(y2 + R2)1/2]
E(y) = (σy/2εo)[1/(y2)1/2 - 1/(y2 + R2)1/2]
2.4. cylinder charge
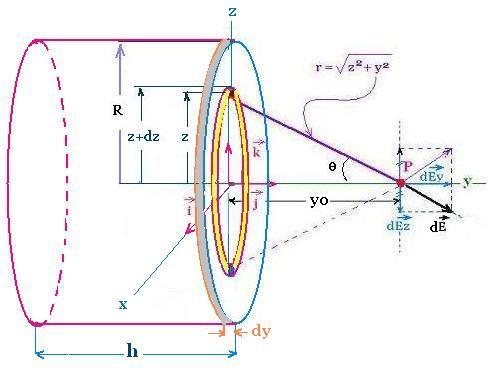
From the formula of the surface charge, we determine the
electric field at the point y due to the whole cylinder
of depth h.
The electric field for a disk, found above, becomes
the elementary electric field for the cylinder.
dE(y:cylinder) = E(y:surface charge) =
(σy/2εo)[1/(y2)1/2 - 1/(y2 + R2)1/2]
Using the relationship:
σ = ρ dy
where
ρ is the volume charge density, we obtain:
dE(y:cylinder) =
(ρy/2εo)[1/(y2)1/2 - 1/(y2 + R2)1/2 dy
dy goes from yo + h to yo
Therefore
E(y) = ∫ E(y:surface charge)
| |
yo
| |
| E(y) = ∫ | |
(ρy/2εo)[1/(y2)1/2 - 1/(y2 + R2)1/2] dy
|
| |
yo + h
| |
| |
yo
| |
| = (ρ/2εo)∫ | |
y[1/(y2)1/2 - 1/(y2 + R2)1/2] dy
|
| |
yo + h
| |
We have:
∫ y[1/(y2)1/2 dy = y
∫ - y/(y2 + R2)1/2 dy =
- (y2 + R2)2
Therefore
| |
yo
| |
| E(y) = (ρ/2εo)∫ | |
y[1/(y2)1/2 - 1/(y2 + R2)1/2] dy
|
| |
yo + h
| |
= (ρ/2εo)[- h + [(yo + h)2 + R2]2 - [yo2 + R2]2]
E(y) = (ρ/2εo)[- h + [(yo + h)2 + R2]2 - (yo2 + R2)2]
|
|