DC current Electric energy and power
1. Power dissipated in a dc circuit element
The electric energy in a circuit supplied by an electric
source is used by the elements in the circuit. The element
in the circuit transforms the energy received by decreasing
the potential through this element.
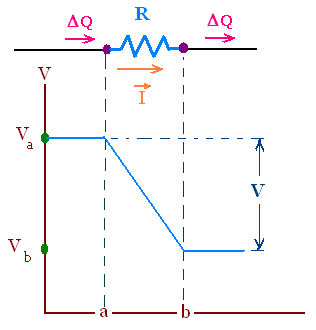
If a current passes through the element ab, the
potential decreases, the potential difference
Vb - Va is negative.
In a time interval Δt, the number of charge carriers with
total charge ΔQ that enters the element at the terminal a of
potential Va is the same as that leaves the element at
the terminal b of potential Vb. That is the current I
= ΔQ/Δt is constant.
The electric potential energy at the terminal a is Ua
= ΔQ Va, and the terminal b is Ub
= ΔQ Vb.
The change in the electric potential
energy is ΔU = Ub - Ua =
ΔQ (Vb - Va) = - ΔQ (Va - Vb).
Va - Vb is positive and denoted by V. Hence
ΔU = - ΔQ V
The rate at which the carriers lose electric potential
energy is - ΔU/Δt. This rate is called the
power dissipated in the element. It is equal to
= + ΔQ/Δt V = VI, therefore.
Power dissipated in a dc circuit element:
P = V I
The dimension of V is the Volt (V), that is the energy
per unit charge; and the dimension of I is the Ampere (A),
that charge per unit time. Hence their product has the
dimension of V A, that is (energy/charge) x (charge/time) =
energy/time, that is power.
2. Energy dissipated in a resistor
The energy transformed by a resistor of resistance R,
when it carries a current I. The charge carriers lose
electric potential energy when they pass through this resistor.
The related dissipated power is
PR = V I = R I I = R I2, called
Joule's law.
Since V = R I, we have also PR = V2/R.
Joule's law for a resistor of resistance R in a dc circuit element:
PR = R I2 = V2/R
The lost electric potential energy of the charge carriers in
the resistor is due chiefly to the collisions of the carriers within
the resistor while the resistor is carrying a current. This is what makes
resistance for a resistor. These collisions are responsible for the increase of the temperature in the resistor. The resistor transfers heat to its surroundings
if its temperature rises above that of its surroundings. The carriers lose
energy that is transferred as heat to the surroundings. Electric energy is dissipated as heat in a resistor, called Joule heating.
3. Energy in a battery
We want to determine the related transformation of
energy in a battery while a current exists in the battery.
3.1. Discharging battery: Energy from a battery
Consider a discharging battery. The charge carriers
pass through the battery in the direction of its emf ℰ.
The potential across the battery increases, hence the potential
difference across the battery is positive. The rate at
which the carriers gain potential energy is + ΔU/Δt.
The potential difference V between the terminals of the battery is
V = ℰ - r I (r is the internal resistance of the battery, and
I is the current that passes through the discharging battery. The
battery is being discharged,hence the energy is supplied; we call
the gained potential energy + ΔU/Δt, the power output
Po from the battery. Therefore
Po = VI = (ℰ - r I) I = ℰI - rI2
Power output from a discharging battery:
Po = VI = (ℰ - r I) I = ℰI - rI2 =
Pℰ - Pr
The term Pℰ = ℰI represents the rate at which
the electric potential energy of the carriers is increased by chemical
reactions in the battery, that is the power expended by the emf
of the battery.
The term Pr = rI2 is the Joule heating or the
energy dissipated as heat due to the internal resistance r of the battery.
While it is discharging, the temperature of the battery increases.
3.2. Charging battery: Energy to a battery
If a battery is being charged, then the sense of the current is
opposite the sense of the battery's emf. Hence V = ℰ + r I, and
Pi = VI = (ℰ +r I) I = ℰI + rI2 =
Pℰ + Pr. Pi is called the Power
input to a charging battery. Pℰ represents the
power delivered to the emf of the battery by the charge carriers.
4. Energy in a circuit element
In any type of circuit element, if V is the potential
difference across the element and I is the current in
the element, Then the rate of energy transformation is
P = V I. It is the rate at which the electric potential
energy of the carriers changes as they pass through the
element.
Power of any circuit element = Rate at which energy is transformed in
a circuit element:
P = VI
|