Electrostatics: Electric potential
1. Introduction
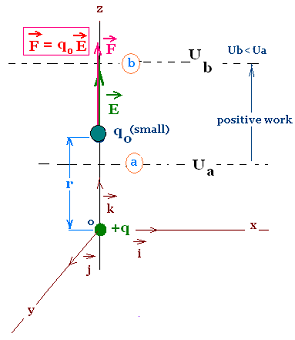
We have defined the vector electric field E as the vector
electric Coulomb's force F per unit of test charge
qo: E = F/qo.
We introduce another field called electric potential
or simply potential V defined as a electric potential
energy per unit charge.
The potential energy is a scalar, so is the potential field V.
The vector electric field E and the scalar electric potential V
are derivable from to another. The electric potential difference
between two points is known as the voltage measured in
Volt. The SI unit of the electric potential energy is Joule,
therefore the SI unit of the potential is Joule/Coulomb = Volt.
2. Work done by electric force on
test charged particle
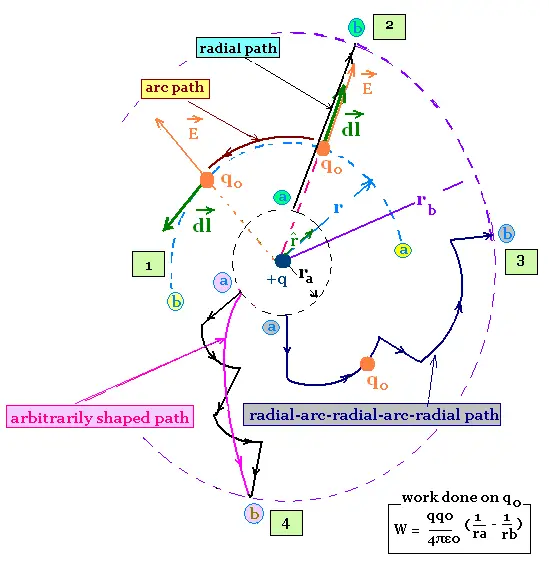
Consider a test charged particle qo moving
in the electric potential field due to the point charge q. The
electric force on the test charge is F = E/qo.
The two vectors F and E are parallels.
2.1. Along circular arc
1. The work done by the electric force F on the test charged
particle moving along a circular arc, from a to b, centred
at the fixed point charge q is:
W = ∫ F. dl = ∫ F dl cos (F, dl) = 0, because
dl is perpendicular to E at each point on the path.
2.2. Along radial path
2. The work done by the electric force F on the test charged
particle moving along a radial path , from a to b is:
W = ∫ F. dl = ∫ F dl , because
dl is parallel to E at each point on this radial path.
F = (1/4πεo) qqo/r2
E = F/qo
The infinitesimal displacement dl = dr ^r, therefore
W = qo∫ E. dl =
(1/4πεo) qqo/r2 dr
| |
rb
| |
| W = (qqo/4πεo) ∫ | |
1/r2 dr =
(qqo/4πεo)
(1/ra - 1/rb)
|
| |
ra
| |
2.3. Along radial-arc path
The path from a to b encounters arc-path with W = 0 and
radial-path with W = ∫F.dl. Since the the terms between
those related to ra and rb cancel out,
the contributions of all the arc-paths is zero and of all
the radial-paths gives:
W = (qqo/4πεo) (1/ra - 1/rb)
The result is independent on any point between a and b.
2.4. Along arbitrarily shaped path
Any arbitrarily shaped path, between a and b, can be viewed
as an infinite number of infinitesimal arc paths and radial paths.
Only the radial-paths contributions survive and the work
done on the particle test by the force F between a and b is
again dependent only on 1/rb and 1/rb.
Work done on the test charge qo moving from a to b:
W = (qqo/4πεo) (1/ra - 1/rb)
The work done on a small test charged particle by an electric force
in an electric field due to a fixed point charge depends
only on the separation distance between the particles before the
displacement (ra) and and after the displacement (rb).
The work done is independent of the path. If the work done by
a force is independent of the path, the force is conservative,
and the change in potential energy is the negative of the work
done by the conservative force :
| |
b
| |
| W = ∫ | |
F.dl = Ua - Ub = - (Ub - Ua) = - ΔU
|
| |
a
| |
3. Electric potential energy
3.1. Test particle in the field of a point charge
The work done by an electric force, which is conservative, in
an electric field, due to a point fixed charge q, on a test charged
particle qo moving from a to b is equal to the
negative of the change in the test particle's potential energy :
W = - ( Ub - Ua) = Ua - Ub, with
Ua = (qqo/4πεo) (1/ra)
And
Ua = (qqo/4πεo) (1/rb)
We can find a general expression of U at any point selecting a
reference position at which the potential energy is zero. The
simple choice is ra = ∞ and rb = r, so
Ua = 0 and Ub = U(r), that is
| |
r
| |
| U(r) = - ∫ | |
F.dl = qoq/4πεor
|
| |
∞
| |
U(r) is the electric potential energy of the
charged test particle qo on the electric
field due to the fixed charge point + q.
3.2. Test particle
in the field of a number of point fixed charges
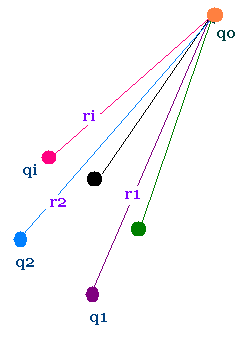
Consider a test particle qo moving from a to b
in the field due to two points fixed charges q1 and q2
distant r1 and r2 from qo respectively.
According to the principle of superposition, the work
done on the test particle by the net electric force conservative
F of the two contributions of the field due to q1 and q2 is:
| |
b
| |
|
b
| |
|
b
| |
|
b
| |
| W = ∫ | | F.dl =
|
∫ | |
qo (E1 + E2).dl =
|
qo∫ | | E1.dl +
|
qo∫ | | E2.dl
|
| |
a
| |
|
a
| |
|
a
| |
|
a
| |
The corresponding potential energy is U = - W:
U = U1 + U2 = (qo/4πεo) (q1/r1 + q2/r2)
r1 and r2 are the distances between the test charge and the
two fixed point charge q1 and q2 respectively.
Extending to a case of more that two fixed particles, we have:
U = (qo/4πεo) Σqi/ri
Where ri is the distances between the test charge and the
fixed point charge i.
Test particle
in the field of a number of point fixed charges:
U = (qo/4πεo) Σqi/ri
3.3. Potential energy in a constant field
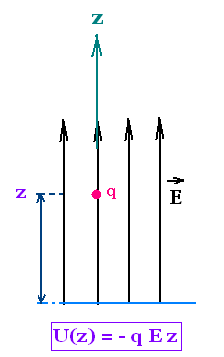
The negative of the work done on a moving charge q from a to b, by an electric force F, due an electric field E is the change in the elctric potential energy of the this charge:
| |
rb
| |
| - W = Ub - Ua = - ∫ | |
F.dl = q E Δl
|
| |
ra
| |
If E is constant in the z direction
Ub - Ua = -
q E (zb - za)
At a point z, we write:
Uz = - q E z
Potential energy of a charge at the position z in a constant electric field E:
Uz = - q E z
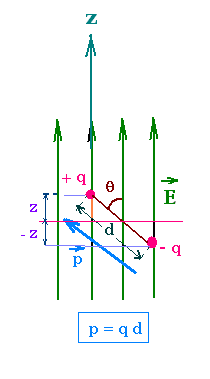
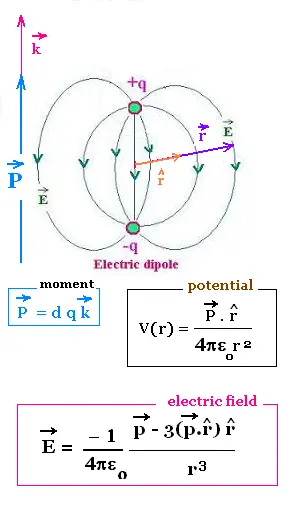
For a dipole of dipole moment:
p = d q ,
the potential energy is U = U(+ q) + U(- q) =
- q E z + - (- q) E (- z) = - 2 q E z = - 2 q E (d/2) cos θ = - q d E cos θ =
- p E cos θ = - p . E
4. Electric potential
4.1. Definition
We defined the electric field E of a fixed charge q as
the ratio of the electric force exerted on a small charged
particle test and its charge qo, by E = F/qo. It is important
that the charge qo used to measure the electric field E
to be small to not alter the charge distribution that
produced the potential due to the fixed charge q.
Similarly, we define the electric potential or potential
V as the ratio of the electric potential energy U and the charge test qo.
V = U/qo
From the above expression of the electric potential energy, we have:
V(r) = U(r)/qo = q/4πεor
for a single fixed charge, and
V(r) = U(r)/qo = (1/4πεo) Σqi/ri
for a distribution of fixed charged particles
Electric potential field:
single fixed charge:
V(r) = q/4πεor
distribution of fixed charged particles:
V(r) = (1/4πεo) Σqi/ri
V(r) as U(r) is a scalar quantity. The potential V(r) has
a value at each point in space where the fixed charge
is present. The SI unit of U(r) is the Joule.
The SI unit of the potential is the Joule/Coulomb = Volt (J/C = V).
Once we know the value of the potential V(r) at the point at the
distance r from the fixed charge producing V(r), we can determine
the potential energy U(r) = qo V(r) for a charge qo.
The charge of elementary particles as electrons and protons is
small. The charge of electron is e = 1.6 x 10- 19 Coulomb.
From this value, we define the unit of energy called the electron-Volt (eV).
1 eV = 1.6 x 10- 19 J.
4.2. Example 1: Distribution of three charges
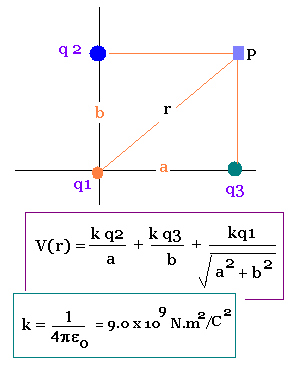
1 N.m/C = 1 J/C = 1 V
1 nC = 1 x 10-9 C
q1 = + 5 nC, q2 + 3 nC, and q3 = - 4 nC.
a = 3 cm , b = 4 cm → r = 5 cm
V(r) = k (3/3 - 4/4 + 5/5 ) =
9.0 x 109N.m2/C2 . 1 nC/cm =
9.0 x 109N.m2/C2 .
1 x 10-9C/10-2m =
9.0 x 102 V = 900 V.
4.3. Example 2: Dipole's potential
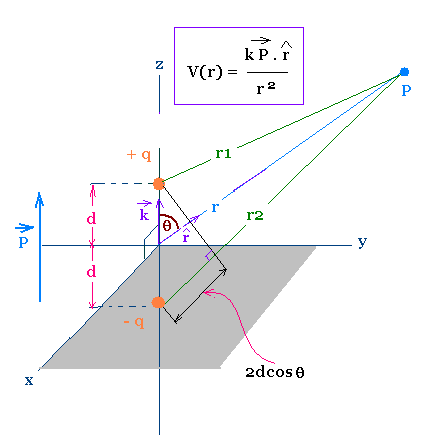
The dipole of moment p = 2dq k^ located at the origin. We want
to determine the potential produced by the dipole far from
the two charges + q and - q , that is at a distance r greater than
the separation 2d between the two charges.
At the point P, we have:
V(r) = (1/4πεo) Σqi/ri =
V(r) = (1/4πεo) q(1/r1 - 1/r2)
Far from the dipole: r ≫d, we can write:
r1 ≈ r2 ≈ r, and
r2 ≈ r1 + 2 d cos θ
Therefore
V(r) = (1/4πεo) 2 q d cos θ(r2 - r1)/r1r2 ≈
(1/4πεo) 2q d cos θ/r2
= (1/4πεo) p cos θ/r2
= (1/4πεo) p . r^ /r2
At θ = 90° V(r) = 0. The potential is zero at all points
in the plane xy, positive at all points above xy plane, and
negative at all points below the xy plane.
Potential due to a dipole:
V(r) = (1/4πεo) 2q d cos θ/r2
4.4. Potential due to continuous charge distribution
The potential for a number of point fixed charges is:
V(r) = (1/4πεo) Σqi/ri
We transform this equation into the equation for a
continuous charge distribution. The continuous charge
distribution is considered as a large number "n" of individual fixed
charges qi. In the limit when n tends to infinity, the sum becomes an
integral:
| | | | n | | | | | |
| V = lim | (1/4πεo) | | Σ | qi/ri | = (1/4πεo)∫ | | dq/r | |
| n → ∞ | | | i=1 | | | | | |
Potential due to continuous
charge distribution :
V(r) = (1/4πεo)∫ dq/r
r is the distance from dq to the point at which the
potential is evaluated.
4.5. Potential due to uniformly charged circular ring
Consider a uniformly charged circular ring of radius R and total
charge Q.
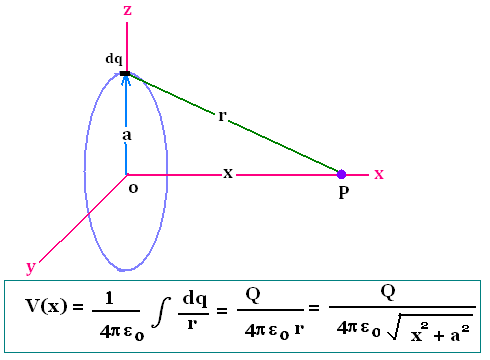
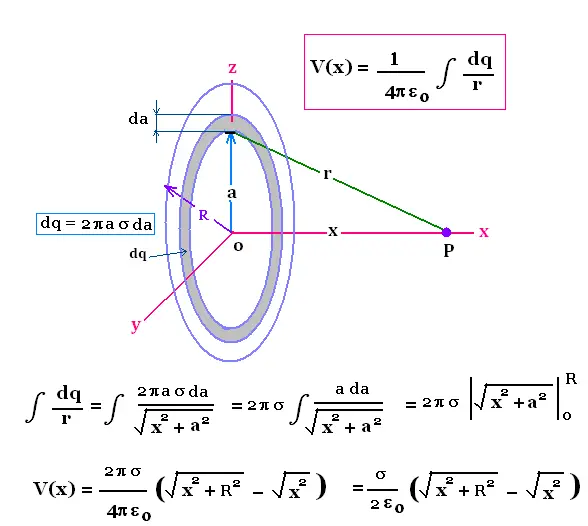
4.6. Potential due to a thin uniformly charged disk
Consider a uniformly charged disk of radius R and surface
cahrge density σ. .
5. Potential difference
5.1. Definition
We have defined the potential energy U with the reference position
at ∞, where U = 0. The potential V is also zero at ∞, and
takes also r = ∞ as the reference position.
Note that a potential energy or potential are just mathematical
functions, but a change in potential energy and a change in potential
has a physical significance. (an abject in a free-fall motion has
a potential energy related to a certain reference position).
The potential difference between two points, that is
the change in potential does not need to use the reference position
V∞ = 0.
If Ub - Ua represents the electric potential energy difference of a
small test charge qo moving from a point a to a point b in the field
due a fixed charge distribution, then the corresponding potential
difference is:
Vb - Va = (Ub - Ua)/qo
The difference in the electric potential energy of a test charge qo
is the negative of the work done by the electric force on this charge.
So
| |
b
| |
| Ub - Ua = - qo ∫ | |
E.dl
|
| |
a
| |
Therefore
Further, we see that the SI unit of the potential is also
the Volt/meter (V/m).
5.2. Application: Uniform electric field
The potential difference between two points a and b
in a uniform field E along the x-axis is:
| |
b
| |
| Vb - Va = - E ∫ | |
dl = - E (xb - xa)
|
| |
a
| |
5.3. Potential difference in a parallel-plate capacitor
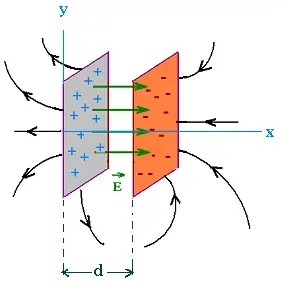
Conside a capacitor formed by two parallel plates. The potential
difference between the two plates is the same as between two points a and b
in a uniform field E along the x-axis :
| |
b
| |
| Vb - Va = - E ∫ | |
dl = - E (xb - xa) = - E d
|
| |
a
| |
The lateral dimension of each plate are much larger than the
plate separation d between the plates. the electric fiels E is
then uniform and it is equal to σ/εo.
Therefore V(x) = Va - Vb = E d
5.4. Potential of a uniformly
charged sphere
Consider a sphere uniformly charged of radius R and charge Q.
We have determined the expression of the elctric field
due to a uniformly charged sphere:
E(inside) = Qr/4πrεoR3
= (ρ/3εo) r
E(outside) = Q/4πεo(1/r2)
= ρR3/3εo(1/r2)
Therefore, the expression of the related potential are:
V(inside)
| |
b
| |
| Vb - Va = - ∫ | |
Qr/4πεoR3 dr =
Q/8πεoR3[ra2 - rb2]
|
| |
a
| |
V(outside)
| |
b
| |
| Vb - Va = - ∫ | |
Q/4πεo(1/r2) dr =
Q/4πεo[1/rb - 1/ra]
|
| |
a
| |
6. Electric field and potential
6.1. Definition
The potential is defined as
r = ∞ is the reference position that
corresponds to V∞ = 0
The position r is the distance between the fixed
charge and the test charge, that is where the potential
is avaluated.
Thus the potential is the negative of the line integral
of the electric field from ∞ to where is evaluated.
We are interested in the reverse operation. Given a potential
V, how tho determine the corresponding electric field E?
Consider an infinitesimal change of the potential in the x
direction dV = V(x + dx) - V(x). The electric field E is
nearly constant and the above integral becomes:
| |
x+dx
| |
| dV = - Ex ∫ | |
dx = - Ex(x' + dx' - x') = - Ex dx
|
| |
x
| |
Thus
dV = - Ex dx
with y and z held constant. Therefore
∂V - Ex ∂x
Similarly
∂V = - Ey ∂y, and
∂V = - Ez ∂z
V and E with cartesian coordinates:
∂V = - Ex ∂x
∂V = - Ey ∂y
∂V = - Ez ∂z
So, the components of E are given by the negative
of the partial derivatives of V.
In the case of a charge distribution with spherical
symmetry, V depends only on the radial coordinate r, so
E has only a radial coordinate, we have:
∂V = - Er ∂r
V and E with radial component:
∂V = - Er ∂r
6.2. Example Electric dipole

We have found the expression of the potential for a dipole
of moment p = 2dq k^, V(r) = (1/4πεo) 2q d cos θ/r2
In cartesian ccordinates
r2 = x2 + y2 + z2
cos θ = z/r = z/[x2 + y2 + z2 ]1/2
The expression of V becomes:
V(r) = (1/4πεo) p z/[x2 + y2 + z2 ]3/2
We have
- ∂V/∂x = Ex = (p/4πεo) 3xz/r5
- ∂V/∂y = Ey = (p/4πεo) 3yz/r5
- ∂V/∂z = Ez = (p/4πεo)
(3z2/r5 - 1/r3)
6.3. Other expression of the electric
field
around a dipole:
E = - ∇V
That is
E = - (∂V/∂x, ∂V/∂y, ∂V/∂z)
V = (1/4πεo) p.r/r3
= (1/4πεo)
(xpx + ypy + zpz)/
(x2 + y2 + z2)3/2
Differentiating with respect to x, gives:
∂V/∂x = (1/4πεo)
[px(x2 + y2 + z2)3/2 - (3/2)(2x)
(xpx + ypy + zpz)
(x2 + y2 + z2)1/2]/
(x2 + y2 + z2)3 =
(1/4πεo)[
px/(x2 + y2 + z23/2 - (3/2)(2x)
(xpx + ypy + zpz)/
(x2 + y2 + z2)5/2]
∂V/∂x = (1/4πεo)[px/r3
- (3x)(p.r)/r5]
Similarly,
∂V/∂y = (1/4πεo)[py/r3
- (3x)(p.r)/r5]
∂V/∂z = (1/4πεo)[pz/r3
- (3x)(p.r)/r5]
Therefore
E = - ∇V = -
(1/4πεo)[p/r3 - (3r)(p.r)]/r5
E = - ∇V = -
(1/4πεo)[p - 3(p.r^)r^]/r3
r^ is the unit vector position.
Electric field around a dipole:
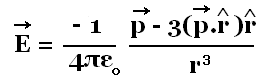
|