|
Electrostatics
Electromagnetics
Electricity &
Magnetism
© The scientific sentence. 2010
| Induced electric fields
1. Varying magnetic field dB(t)/dt
generates electric field E
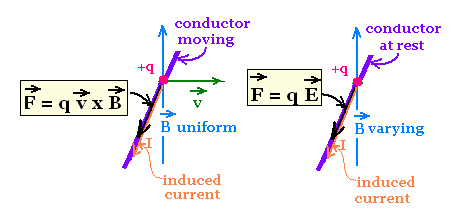
Consider a conductor moving at a velocity v crossing a
uniform magnetic field B. A charge q inside the conducor experiences
a magnetic force Fm = qv x B perpendicular to the plane
of v and B. This magnetic force on the charge is reponsible of the
induced current.
Now, if the conductor is at rest and we vary the magnetic field,
an induced current is produced in the conductor.
what is then the force responsible of the motion of the charge?
If it is not Fm = qv x B, because the conductor
is fixed and then the velocity of the charge is zero
before the current is induced, It must be an electric force
Fe = qE and then an electric field must be present
the long of the conductor to drive the charge when the magnetic
field is changing.
2. Integral form of Faraday's law
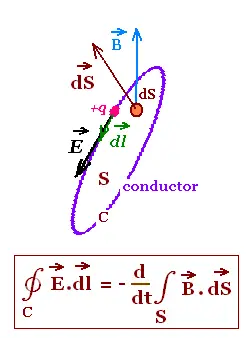
A varying magnetic field B(t), linking a loop or coil (conductor)
of contour C and surface S, causes an emf ℰ = - dΦB/dt;
within this conductor; that is an induced current the
long of the this conductor. This induced current is the displacement of charges (q)
due to an electric force F = q E due to the existence of an induced electric field E.
The induced emf ℰ is a potential difference (in Volt). The work done
by the charge q along the contour C is W = q ℰ.
The infinitesimal work done by the charge q along the element dl is:
→ → → →
F . dl = q E.dl
Along the contour C, which is the closed path conducting
circuit, the work done by the force is
→ →
W = ∮ q E.dl = qℰ
Faraday's law becomes
→ →
ℰ = ∮ E.dl = - dΦB/dt.
The induced emf ℰ in the circuit is a direct consequence
of the induced electric field E. Since
→ →
ΦB = ∫ B.dS, the flux through any surface
bounded by the related closed path,
we get
→ →
→ →
∮E.dl = - d(∫B.dS)/dt
That is the integral form of Faraday's law.
→ →
→ →
∮E.dl = - d(∫B.dS)/dt
Of course, the induced electric field has a nonzero closed-path
line integral as it is for an electrostatic field which is conservative.
Induced electric field and electrodtatic field are different from each other.
An electrostatic field is produced by static distribution of charge
and determined via Coulomb's law. An induced electric field is a
nonconservative electric field.
The induced electric field is the nonconservative
electric field produed by a changing magnetic field.
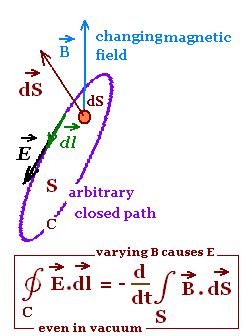
The chosen closed-path coincides with the conducting loop,
where we have the emf ℰ. Outside the wire,
there is no emf ℰ , but the induced electric field
is present. The integral form of Fraday's law is valid even
if no conductor is present in the region.
|
|