Electrostatic properties of insulators

1. Insulator as dielectric

The insulator considered here is the nonconducting material filling the space between the two plates of a capacitor. In this case the insulator is called dielectric. Under these conditions, the dielectric provides electrostatic properties of an insulator.

The experiments show that the potential difference in vacuum between the plates of a charged capacitor decreases when we replace the vacuum by an insulator such as plastic or glass. If we remove the dielectric, the potential difference increases and returns it initial value, when the dielectric was vacuum.

The effect of decreasing the potential difference from V_o (when dielectric is vacuum) to V (when the dielectric is other insulator) is not attributed to the reduction of charge of the capacitor, because the potential difference returns to its initial value after removing the insulator. Changing the dielectric alters just the electric field.

Experiments with different types of insulating materials show the ratio V_o/V depends on the type of the used material. This ratio is denoted by Κ and called dielectric constant Κ

Κ = V_o/V

For example, at 20°C

Κ(vacuum) = 1
Κ(air) = 1
Κ(Benzene) 3.1
Κ(water) = 80
Κ(nylon) = 3.4
Κ(paper) = 3.6

Since V_o = E_od and V = E d when the dielectric is inserted, we have:

Κ V_o/V = E_o/E

Κ = E_o/E

Since V = Q/C and V_o = Q/C_o, we have:

Κ V_o/V = Q/C_o/(Q/C)= C/C_o

Κ = C/C_o

The insertion of a dielectric causes the capacitance to be increased by a factor Κ.

Since U = QV/2 and U_o = QV_o/2, we have:

Κ V_o/V = (2U_o/Q) / 2U/Q = U_o/ U

Κ = U_o/U

The insertion of a dielectric causes the capacitor's energy to be decreased by a factor Κ.

2. Atomic description of an insulator

When we disconnect a capacitor from the charging battery, that is once the capacitor is charged; and we place a dielectric between the plates of a charged capacitor, the electric field is reduced even though the charge on the plates remains fixed.

If the field is reduced, that would come only from the reduction of the related charges. As the charges on the plates remains fixed, there will exist other charges inside the dielectric responsible for this reduction of the field. The charges that cause the reduction of the field are called bound charges or polarization charges. These charges reside on the surface of the dielectric.

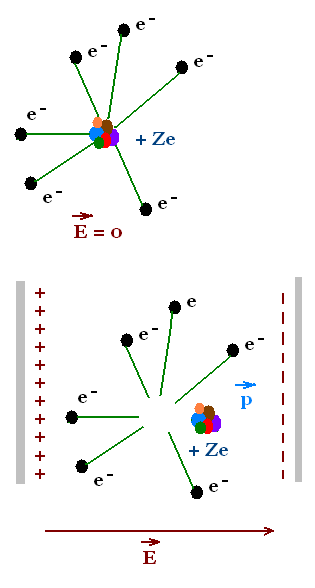
A neutral atom contains a nucleus with Z protons of charge + Ze, that is the point charge that occupies the center of the atom, surrounded by a spherically symmetric distribution of negative charge - Ze due to the Z electrons. The electric attraction between the electrons and the nucleus makes the center of negative charge distribution coincides with the position of the nucleus.



When the atom is placed in an external electric field E, this electric field exerts forces on the nucleus and electrons, that are opposite in direction. At equilibrium, the electrons and the nucleus are subjected to two forces: the force due to the external field E_b, that tends to separate the electrons from the nucleus and the Coulomb's forces that tends to superimpose the nucleus and the center of the negative charge distribution. As a result of the external field, the position of the nucleus and the center of the negative charge distribution become displaced. The atom acquires an induced dipole, hence it becomes polarized.

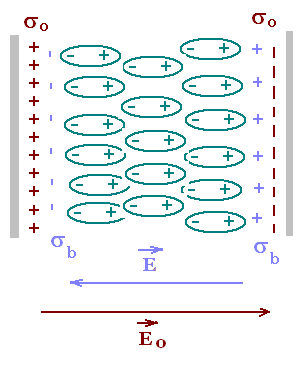
When a dielectric slab is placed in the uniform field E_b between the plates of a parallel-plate capacitor, the dielectric becomes polarized because dipoles are induced and aligned in it by the applied external field. This induced polarization generates an accumulation of charges of opposite sign on the faces of the dielectric, adjacent to the plates. The sign of the induced charge on each slab face is opposite that of the charge on its adjacent plate.

At each plate of the capacitor, we have two surface charges density: σ_b due to the induced bound charges, and σ_o due to the charged capacitor when it was previously connected to the battery. Note that σ_o remains unaffected by the insertion of the dielectric while the battery is disconnected.

The electric field E in the dielectric has now two contributions E_o due to σ_o and E_b due to σ_b. We have

E_o = σ_o/ε_o, and E_b = σ_b/ε_o.

Note that E_o is the same field that was present before the insertion of the dielectric.

This two contributions to the field E are in opposite direction:

The vectorial sum is:
→   →    →
E = E_o + E_b

The magnitude of E is E = E_o - E_b = (1/ε_o)(σ_o - σ_b)

Since Κ = E_o/E , we obtain E = (1/ε_o)(σ_o - σ_b) = E_o/Κ

Solving for σ_b, we get:

(Κ/E_oε_o)(σ_o - σ_b) = 1 , or

σ_b = σ_o(Κ - 1)/Κ

Since the factor (Κ - 1)/Κ is less than 1, σ_b is less that σ_o.