Line of fields

The spatial distribution of a field in a region is represented by lines of field.
The number of lines, crossing a surface perpendicular to the lines, per unit area, is called density of lines.

1. Gravitational field

Gravity is the gravitational field. The gravitational field g at a point P is defined as the gravitational force (weight) F on a particle located at P divided by the mass m of the particle; that the gravitational force per unit mass.
→   →
g = F/m



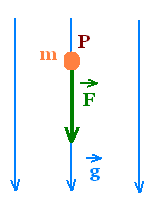
We are familiar with the gravitational field of the earth, where the vector g is called the acceleration due to gravity. This vector acceleration is directed vertically downward. It has the expression:
→          →
g = - 9.81 j
→
j is the unit vector directed upward away from the center of earth. The quantity 9.81 m/s² is the value of the gravitational field of the earth at a point near the surface of the earth.



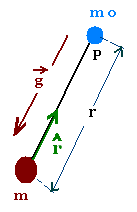
Any mass other than the earth has a gravitational field. Let's consider a particle with mass m and another particle (test particle) of mass m_o. The two masses attract each other in accordance to Newton's law of gravitation:
m_o g = Gm_om/r².

Therefore

The gravitational field g of the mass m is:
g = G m/r²

→             ^
g = - (Gm/r²) r

r is the distance from the center of the object of mass m to the point P where the field is evaluated, and ^r is the unit vector directed away from the center of the object and toward the point P.



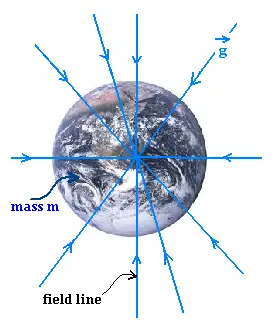
The gravitational field lines are radial.
The field g is tangent to the line at each point on the line. The lines are directed away from a test mass toward a point mass.
The spacing in the drawn lines indicates the magnitude of the field. Where the lines are close together, or dense,the field g is large; and where they are far apart, the field g is small as inside the earth.
The density of lines is proportional to the field g, then to the mass m.

2. Electric field

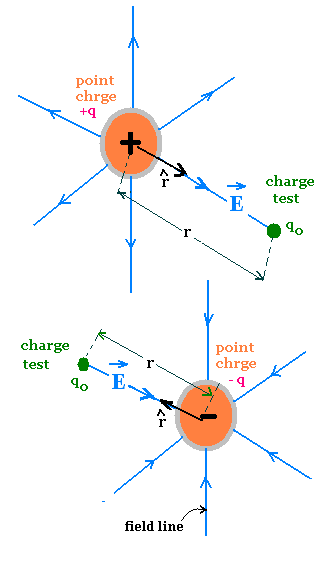
As a gravitational field, the electric field is a vector quantity. If a test charge particle q_o is placed at a point P at a distance R from a charge particle q, then the electric field E at the point P due to the charge q is defined as the electric force F exerted by the charge q on the test charge particle divided by the test particle's charge q_o. That is
→   →
E = F/q_o

From Coulomb's law

→            ^
E =(q/4πε_or²)r


The electric field lines are radial.
The field E is tangent to the line at each point on the line. The lines are directed away from a positive charge and toward a negative charge.

The spacing in the drawn lines indicates the magnitude of the field. Where the lines are close together, or dense, the field E is large; and where they are far apart, the field E is small.
The density of lines is proportional to the field E, then to the charge |q|.

A uniform field is represented by field lines that are equally spaced, straight and parallel.

2. Magnetic field

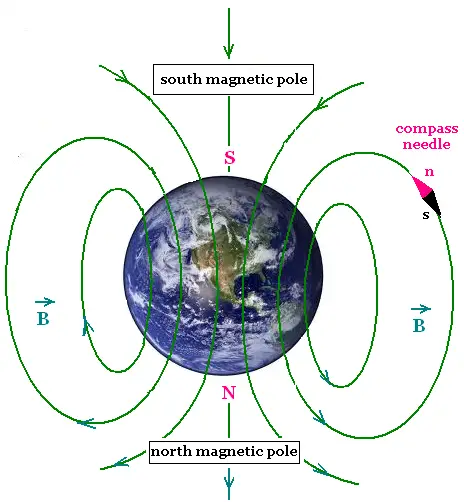
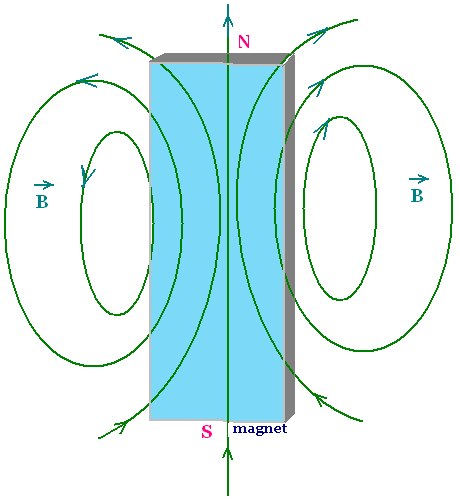
A moving charges, that is electric current is the principal source of magnetic field.

The vector magnetic field exerts a force on a moving charge or a current-carrying conductor.

At a certain point, the magnetic force F _m due to the magnetic field B exerted on the moving particle of charge q is always perpendicular to the velocity v of the moving charge, and perpendicular to the vector field B, that is perpendicular to the plane formed by the vector v and B.



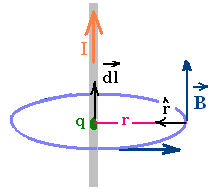
Force on a moving charge:
→      →   →
F_m = q v x B

Force on a set of moving charges:
carrying conductor dl
→      →    →
F_m = ∫Idl x B

Magnetic field of moving charges
carrying conductor dl:
→               →    ^
B = (μ_o/4π)∫ (I dl x r)/r²