Electromagnetics: The magnetic field

Magnets attract small pieces of iron as the earth attracts masses. The magnet produces a magnetic field that attracts charges objects. This interaction is called magnetism.

Electric current is also a source of magnetism, discovered by Hans Christian Oersted in 1891. This is electromagnetism, that is electricity and magnetism. When the current is constant in time, we deal with magnetostatics.

Phenomena related to both electric field and magnetic field deal with electromagnetics, that started with the experiments of Faraday and Joseph Henry. James Clerk Maxwell synthesized all in some equations.

Quantum theory gives a microscopic theory of magnetic materials.

In this chapter, we will consider the effect of a magnetic field on electric charges and currents.

1. The magnetic field

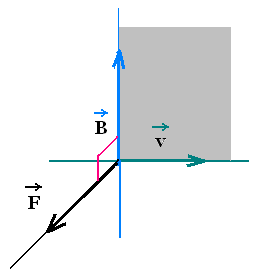
As an electric field E that exerts a force F = q E in a charged particle q, the magnetic field does the same thing for a moving charged particle. Experiments show that the exerted force F by a magnetic field B on a moving charged particle q is directed in the plane perpendicular the plane formed by the velocity v of the particle and the magnetic field B: F ⊥ plane(v,B).

The expression of the magnetic force F is

→		→  →
Fm   = q		v x B = qvB sin θ

θ is the angle between v and B.

The SI unit of magnetic field is Newton/Cm/s = T tesla. We use also the gauss (G).

1 T = 10⁴G. The magnitude of the magnetic field of the earth near the surface is about 0.3 G. In the laboratory, the largest produced is about 30 T.

Note that, if the charged particle is not accelerated, its velocity is constant and any infinitesimal displacement can just be written as dl = v dt, during the time dt. Therefore dl and v are parallel and since F is perpendicular to v, it is also perpendicular to dl, hence the work done by the magnetic force on the charged particle is zero . A static magnetic field does no work on a charge, but an electric field does.

2. Force on a current-carrying conductor

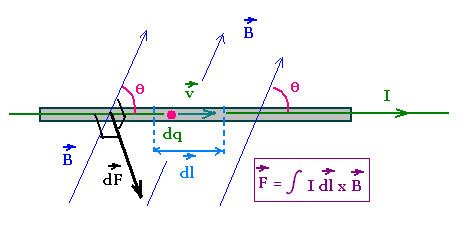
A current in a conductor is a set of charged particles (or charge carriers) moving at certain average velocity v_d called drift velocity.

Therefore, the previous equation can be used to determine the magnetic force on that conductor.

Consider a thin and straight wire crossed by a current I = dq/dt.

So dq = I dt.

Substituting this equation in dF = dq v_d x B, we obtain the infinitesimal magnetic force on the element dl of the wire:

dF = dq v_d x B = I dt v_d x B = I dl x B,
where dl = v_d dt is the infinitesimal displacement of the charge carriers at the drift velocity v_d. I dl is the correspondent infinitesimal current element.

Integrating gives:

F = ∫ I dl x B

3. Magnetic force on a half-ring
current carrying wire

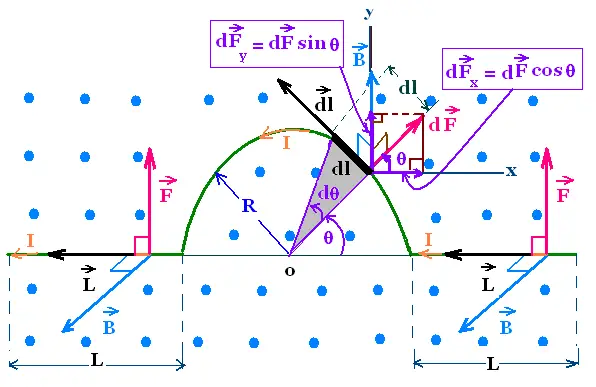
Consider a half-ring wire in a uniform magnetic field B perpendicular to the plane of the figure, that points out. The conductor has two straight segments, at left and at right, with length L parallel to the x-axis. A semicircle of radius R, links the two segments. The conductor carries a current I.

We are interested to find the total magnetic force on the whole wire.

At left and right, both the two magnetic forces are directed upward on the y-axis. Their magnitude has
F_l = F_r = ∫ B I dl sin 90° = B I ∫ dl = B I L each.

Therefore

On the two segments, the magnetic force is
F_s = F_r + F_l = 2 B I L

On the semicircle, the magnetic force dF acts on the element dl = R dθ. This force is "centrifugal".

This force dF has two components:
On x-axis: dF_x = dF cos θ, and
On y-axis: dF_y = dF sin θ

Therefore the force on the entire semicircle has the components:

F_x = ∫ dF cos θ = ∫ I dl x B cos θ =
∫ I R dθ B cos θ = B I R ∫ cos θ dθ

F_x = B I R ∫ cos θ dθ = 0
θ : 0 → π

And

F_y = B I R ∫ sin θ dθ = 2 B I R
θ : 0 → π

F_x = 0
F_y = 2 B I R


The total magnetic force, oriented to the y-axis is then:

F = 2BIL + 2BIR = BI(2L + 2R)

It is exactly the same force if we replace the semicircle with a straight segment along the x-axis between the ones on the left and the right.

4. Torque on a current loop

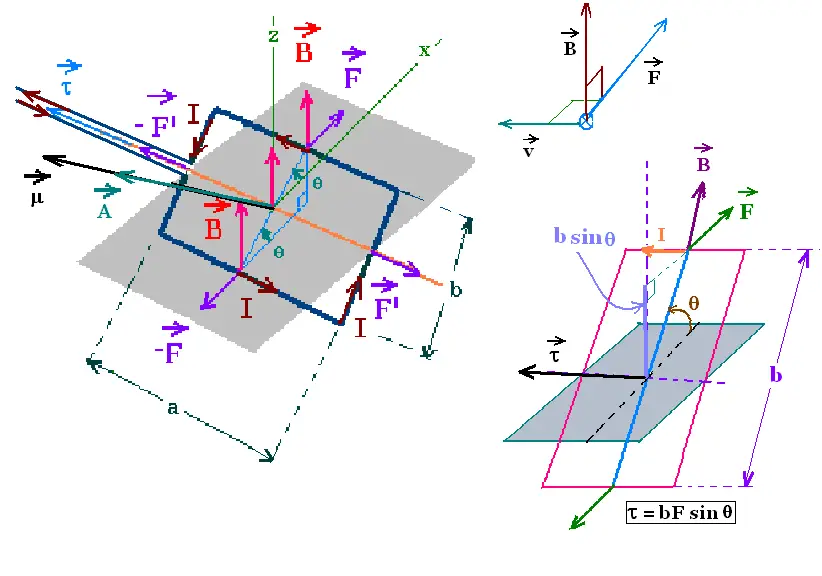
A magnetic field exerts a force on a current carrying wire. About an axis, in a current loop, the magnetic field produces a torque.

Consider a rectangular loop of dimensions a and b. carrying a current I, in a uniform magnetic B directed down-up.

The area of the plane of the loop is A = ab. The vector area A defines the orientation of the loop. The right hand rule following the sense of the current determine the orientation of the vector A. The direction of A is perpendicular to the plane of the loop.

The magnetic force on each straight segment of the loop is F = ∫ I dl x B = B I ∫ dl = B I l.

on the upper element: F = B I a
on the lower element: - F = B I a
on the right element: F' = B I b
on the left element: - F' = B I b

The two forces (F', - F') add to zero. They produce no torque because they are on the rotation axis.

The two forces (F, - F) add to zero before the loop is pivoted. They produce a torque τ_net on the loop about the x-axis.

The magnitude of the net torque is:

τ_net = τ_F + τ_-F = + F (b/2) sin θ + F (b/2) sin θ = F b sin θ = B I a b sin θ = B I A sin θ.

The right-hand rule gives the direction of the torque which is the direction of the cross product A X B (from the right to the left).

Since θ is the angle between the two vector magnetic field B and the vector area A, the magnetic torque takes the form:

τ_net = IA x B

This result is valid for a loop of any shape carrying a current I, in a uniform magnetic field. Especially for a turn of wire or a coil with N turns forming an area of A. The torque on each turn is τ = IA x B. Thus the torque produced by a coil of N turns is τ_coil = Nτ_turn = NIA x B.

The magnetic torque on the coil of N turns carrying a current I, in a uniform magnetic field B, is :

4. Magnetic dipole moment

The magnitude of the magnetic torque varies with the position of the current carrying. When the the vector A and the vector B are parallel (as the position before pivoting the current loop), the magnetic torque is zero. This position is the rotational equilibrium position of the current loop.

Once the loop leaves this position, the magnetic torque tends to align the current loop at the equilibrium position. This effect occurs, of course, with a bar magnet in a uniform magnetic field in which the torque tends to align the north pole with sense of the magnetic field. This is exactly what it happens with an electric dipole in an electric field.

The orientation of an electric dipole in a uniform electric field is the equilibrium position in which the dipole moment P and the electric field E are aligned.

Since the electric potential energy

U = - P.E = - P E cos θ, then U = 0.
θ is the angle between P and E.

The torque of an electric dipole τ that tends to align P with E is τ = P x E

In analogy, we define a magnetic dipole moment μ of a current carrying conductor, in a uniform magnetic field B by the torque τ applied on this magnetic dipole moment μ as:

→		→  →
τ   =		μ x B

For a coil with N turns, the torque is:
τ = μ x B = NIA x B
Which gives:

μ = NIA

The SI unit of magnetic dipole moment is A.m² .

In analogy with the electric dipole, we define the potential energy for the magnetic dipole

		→     →
U   = -		μ • B

U = - μ . B = - μ B cos θ.
θ is the angle between the vectors μ and B.