Electromagnetics: Motion of charges
in electromagnetic fields

1. Circular path of charged particle

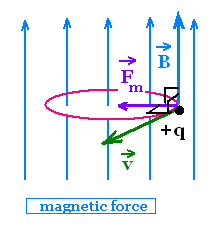
Consider a positive charge +q that starts to move at constant velocity v in a uniform magnetic field B directed upward. The related magnetic force F_m is perpendicular to the plane formed by v and B.

This force is the only force that is acting on the particle. While this force acts on this particle, the trajectory of the particle must change to maintain F, B and V perpendicular to each other. Therefore the particle becomes forced to moves on a circle.

From Newton's second law, the magnetic force is then a centripetal force (radial force) of magnitude F_c = m v²/R. m is the mass of the charged particle, and R is the radius of its circular trajectory.

This force is equal to the magnetic force F_m.

Equating gives:

m v²/R = q v B

Solving for R gives:

R = m v/q B

The angular speed or angular frequency is

ω = v/R = (q/m)B

It depends only on the field B and the charge-to-mass ratio q/m of a given particle.

The operation of a cyclotron is based on this property. This is why the frequency ω is called cyclotron frequency.

2. Lorentz force

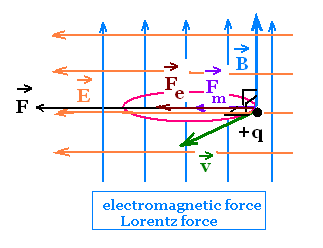
In the case of the charged particle q moves in both electric E and magnetic field B, that is an electromagnetic field, the combined force F that acts on the particle becomes the electromagnetic force that is the vectorial some of F_e and F_m:

F = F_e + F_m = q E + q v x B
That is called Lorentz force.

→		→       →	→
F = q		(E + v x	B)

3. Applications

3.1. The cyclotron

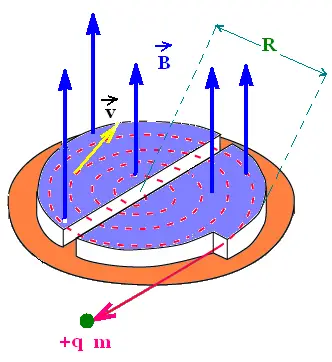
A cyclotron accelerates charges particles. It consists of two D-shaped regions known as dees in a magnetic field, separated by a gap under uniform electric field due to an alternating potential difference.

A charged particle leaves a dee, accelerated across the gap before to reach the other dee. Once accelerated, the particle gain speed, then radius. Under the magnetic field, the path of the particle becomes curved.

The particle returns to the gap at another position and encounters the alternating potential difference across the gap that accelerates it again. The process is repeated until the particle leaves the cyclotron.

The applied accelerating potential difference is maintained in phase with the circulating charge particle, by an oscillator at the same angular frequency ω as the charged particle. The angular frequency of the charged particle, that is the cyclotron frequency of the particle, must match all the time the angular frequency of the oscillator.

A positive charge q of mass m is being accelerated in a cyclotron with a uniform magnetic field B. Its angular frequency ω depends only on the ration (q/m) and B: ω = (q/m)B, hence it remains the same.

The velocity of the charged particle at the last turn, when the radius is R, that is at the outer edge of the dee is v = ω R.

The particle leaves the cyclotron with a kinetic energy KE = (1/2)m v² = (1/2)m (ω R)² = (1/2)m (q/m)²B² R² = q²B² R²/2m.

KE = (qBR)²/2m

The maximum of this kinetic energy is limited when the speed of the particle approaches that of light. The relativistic effects make the frequency ω depends on the speed. In a synchrocyclotron, to overcome this effect, we change the frequency of the oscillator to synchronize, at each cycle, the two frequencies.

For example, an accelerated proton +e emerging from a cyclotron of radius R = 50.00 cm with a magnetic field of magnitude B = 1.5 T has:

• The cyclotron frequency ω = (e/m)B
= (1.6 x 10^-19C/1.67 x 10^-27)1.5 = 1.5 x 10⁸ rad/s

• The speed v = ω R
= 1.5 x 10⁸ (rad/s) . 0.5 (m) = 4.5 x 10⁷ m/s

• The kinetic energy KE = (1/2) m v²
= (1/2) (1.67 x 10^-27)(4.5 x 10⁷)² J = 16.90 x 10^-13 J =
16.90 x 10^-13 eV / 1.6 x 10^-19 = 10.57 x 10⁶ eV = 11 MeV.

3.2. The Hall effect

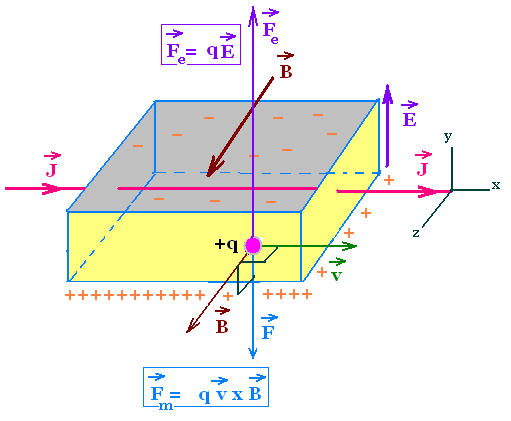
Consoder a current carrying conducter in a form of a strip crossed by an electric current of current density J in a uniform magnetic field B.

Whith a given sense of current (J in x-direction), negative charge (-q) moves in the opposite direction and positive charge in the same direction. In both cases the magnetic force F_m is directed downward. The charges are then accumulated on the lower and upper surfaces.

This charge separation produces an electric field E in the conductor exerting an electric force F_e on the moving charge. The accumulation of the charges continues until the electric force F_e balances the magnetic force F_m in which we reach the steady state. The corresponding electric field is called Hall-field.



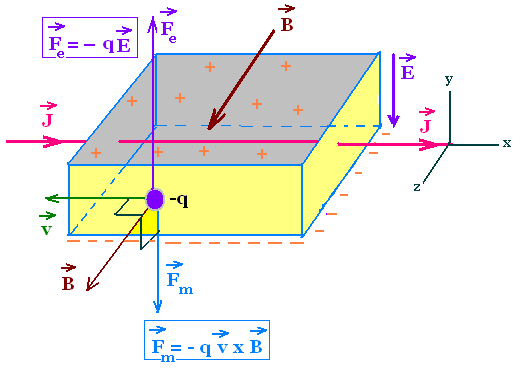
The magnitude of the current density is J = n q v n is the number of carriers per unit volume (or density of carriers) q is the charge of each carrier v is the magnitude of the drift velocity

At the steady state, we have:

q v B = q E , that is

E = v B = JB/nq or


B = E/v = (nq/J)E

Having a device calibrated with a given E and J, the hall effect can be used to determine B in a region by measuring the Hall field.