Motional emf's

1. Motional emf's

In a stationary loop or coil, an emf is induced if the magnetic flux linking it changes. Because the expression of the magnetic flux is:

The magnetic flux can change in three manners:
1 - The magnitude of the field changes, or
2 - The surface crossed by the field changes, or
3 - The orientation of the circuit that link the flux changes.

Changing the orientation of the conductor circuit, or its surface leads to a motional emf. This process converts mechanical energy to electric energy.

2. Applications

2.1. sliding wire circuit

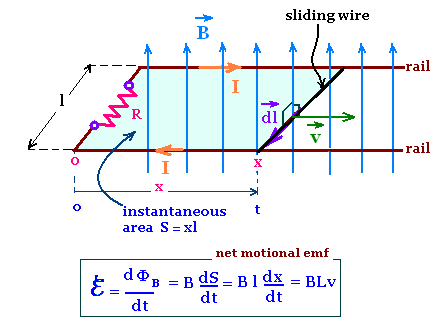
Consider a sliding wire circuit with an U-shaped conductor at rest in a region of uniform magnetic field B perpendicular to the plane of this circuit.

On the two rails of the circuit, moves a conducting wire of length l that slides on the rails of the circuit with a constant velocity v parallel to the rails, then perpendicular to B.

The sliding wire moves, then the charge carriers in it also move. Therefore, the magnetic field exerts a force F on each charge carrier q:
→     →   →
F = q v x B

This magnetic force is responsible of circulating the charge carriers along the circuit. giving rise to an induced current, the an emf ℰ through the resistor R.

The moving charge carriers in the wire are electrons, v x B points in the dl direction, hence F = (- e) v x B points in the opposite direction, thus the sense of the current is in dl direction.

Moving he wire from the left to the right, increases the surface crossed by the magnetic field B from Si = xl to Sf = (x + dx) l, hence the flux Φ_B of the magnetic field B increases from Φ_Bi = B x l to Φ_Bf = (x + dx)Bl.
The change in the magnetic flux is then dΦ_Bi = Φ_Bf - Φ_Bi = B l dx. Therefore, the rate of change of the magnetic field is: dΦ_Bi/dt = B l dx/dt = Blv = ℰ

In addition to the magnetic force, there are other forces (for example due to the Hall effect) that contribute to the net emf ℰ.

2.2. Generators and alternators

Faraday's law is the basis of the conversion of mechanical energy to electrical energy. Electric generators and alternators use this principle of conversion.

2.2.1. Generators

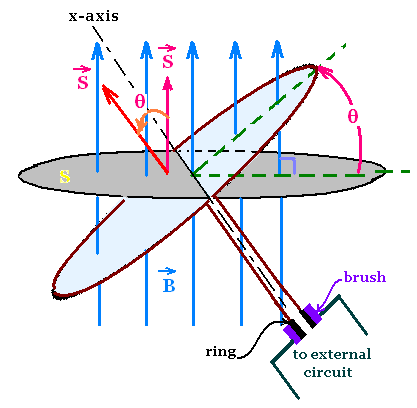
A generator (dynamo) contains mainly a conducting coil rotating in a uniform magnetic field. The induced electric current is collected in an external circuit via brushes on rotating rings.

Consider a simple representation of a generator with a circular loop rotating about the x-axis perpendicular to a uniform magnetic field B.

The flux linking the loop is:
       →  →   → →
Φ_B = ∫ B.dS = B.S = B S cos θ

The loop rotates, then the angle θ is changing, therefore the flux is changing that leads to un emf.

If the loop rotates at constant angular speed ω about the x-axis, then θ = ωt, thus Φ_B = B S cos ωt. The emf becomes:

ℰ = - dΦ_B/dt = B S ω sin ωt.

With n turns in a coil, we have: ℰ = n B S ω sin ωt.

The emf oscillates, the induced current is then an alternating current: ac. So the generator is called an ac generator.

To obtain a direct current or a dc generator, we change the connection. Instead of having two rings as in the ac current, we make connection between the loop and the external circuit with a split-ring commutator. By this switch, the sense of the output voltage remains the same that leads to a dc current.

2.2.2. Alternators

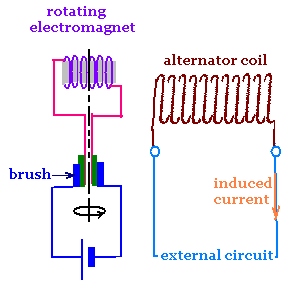
The values of the currents in generators or relatively small because of the large number of turns that leads to a large resistance in the coil circuit. Large values of currents as some ten of Amperes cannot be handled by the electrical contacts like brushes and commutators. To avoid this, we use rotating magnets or rotating electromagnets that induce emf in another stationary coil without sliding contacts or brushes, which will carry the large current in the external circuit. This is the principle of an alternator.
Brushes are used in alternator to supply a smaller currents to rotating electromagnets.