|
Electrostatics
Electromagnetics
Electricity &
Magnetism
© The scientific sentence. 2010
|
Mutual inductance
Mutual inductance
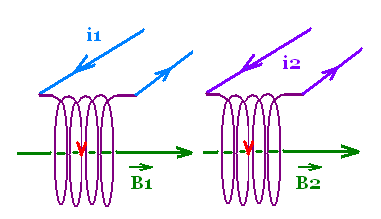
Consider two coils 1 and 2 one
in front of the other, of length l1 and l2, cross-sectional
areas S1 and S2, with n1, and n2 turns per unit length each.
The two coils carry the currents i1 and i2, . The current i1
produces a magnetic field B1 inside the coil 1 that influences
the nearby coil 2.
When i1 changes (then B1 changes), it produces in the coil 1 a self-induced
emf = ℰ11, and a induced emf = ℰ21 in the
coil 2 through (external field) B1.
Similarly, the current i2 produces a magnetic field B2 inside the
coil 2 that influences the nearby coil 1.
when i2 changes in the coil 2 (then B2 changes), it produces in
the coil 2 a self-induced emf = ℰ22, and a induced emf =
ℰ12 in the coil 1 through (external field) B2.
The effect of inducing an emf by one coil on the
other is called mutual induction.
Self-induction in the coil 1
The magnetic field inside is B1 = μo n1 i1
The magnetic flux due to B1 that links this coil is Φ11 = B1 S1
Its emf = ℰ1 = - n1 dΦB1/dt
= - μon12 S1 l1 di1/dt
Its self-inductance is L1 = μon12S1l1
Self-induction in the coil 2
The magnetic field inside is B2 = μo n2 i2
The magnetic flux due to B2 that links this coil is Φ22 = B2 S2
Its self = ℰ2 = - n2 dΦB2/dt
= - μon22 S2 l2 di2/dt
Its self-inductance is L12 = μon22S2l2
Interaction: Mutual-induction of the coil 1 and the coil 2
The magnetic field inside the two coils is B1 + B2 =
μo n2 i2 + μo n1 i1
The magnetic flux due to (B1 + B2) that links this coil 1
is Φ1-12 = (B1 + B2) S1
and the magnetic flux due to (B1 + B2) that links this coil 2
is Φ2-12 = (B1 + B2) S2
The emf of the coil 1 is emf = ℰ12
= - n1 l1 dΦ(B1 + B2)/dt
= - n1 l1 S1 μo d(n2 i2 + n1 i1)/dt
= - n1 l1 S1 μo (n2 di2/dt + n1 di1/dt)
The emf of the coil 2 is emf = ℰ21
= - n2 l2 dΦ(B1 + B2)/dt
= - n12 l2 S2 μo d(n2 i2 + n1 i1)/dt
We define:
The mutual-inductance for the coil 1:
ℰ12 = - M12 di1/dt, and
The mutual-inductance for the coil 2:
ℰ21 = - M21 di2/dt, and
M12 and M21 are called coefficient of mutual inductance.
They depend on the geometrical factors of the coils.
We can consider the particular case where M12 = M21 = M.
M is then the inductance of the pair. The SI unit of the
mutual inductance is the Henry.
|
|