|
Electrostatics
Electromagnetics
Electricity &
Magnetism
© The scientific sentence. 2010
|
Self-inductance and LR circuit
1. Self-induced emf's
Consider a loop or coil carrying a current i. Then it exists, in the vicinity of the loop, an
induced magnetic field B given by the Biot-Savart law. The induced field is proportional to the current i.
The changing magnetic flux Φ linking the loop produces the
emf given by Faraday's law ℰ = - dΦB/dt. We obtain a varying
flux by moving a magnet. But the varying magnetic flux can be also obtained
by varying B then by varying the current i. This process of changing the current
in a circuit (loop's or coil's own current) produces a self-induced emf.
If the magnetic field B induced is proportional to i,
then does the magnetic flux. We write Φ = L i
Faraday's law becomes
ℰL = - dΦB/dt = - L di/dt
The constant of proportionality L is defined as the self-inductance
(or inductance) for the loop.
The SI unit of inductance in the Henry (H). It is a large
unit of inductance. the values of self-inductance of coils in electronic
circuits are typically in the 1µH to a mH range.
2. Example of a solenoid
Solenoid of length l, and cross-sectional area S with
n turns per unit length. The magnitude of the field is
B = μo n i. The flux linking one loop is
ΦB = μo n i S. The flux linking
a solenoid is NΦB , where N = nl.
The emf induced in the N-turn coil solenoid is
ℰL = - N dΦB/dt
= - nl μo n S di/dt
Therefore
L = μon2Sl
L = μon2Sl
That is the self-inductance of an ideal (infinitely long)
solenoid, where we neglect the end effects.
The inductance can be measured in a circuit that
contain the related element as a coil.
3. L R circuit
3.1. Switch at the position 1
At the position 1, the battery is connected; the
current increases during a certain time until it stabilizes
and becomes equal to the steady value I = ℰo/R.
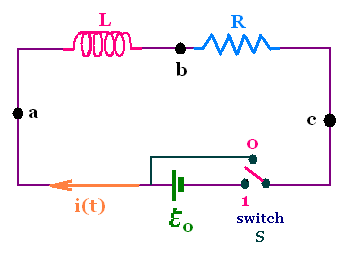
Consider a circuit with a coil or solenoid providing a
self-inductance connected to a battery through a switch. When
the switch is closed, the battery causes charge to move
in the circuit. The solenoid has a self-inductance L and
a resistance R.
As the current i(t) in the circuit changes through the switch,
there is a self-induced emf ℰL = - L di(t)/dt
in the inductance that opposes a change in the current, preventing
it to vary abruptly. The instantaneous value of the current
depends on the value of L, R and the emf of the battery ℰo.
We apply the loop rule: Starting at the point a,
proceeding clockwise, and equating the sum of the voltage
change to zero gives:
(Va - Vc) + (Vb - Va)
+ (Vc - Vb) = 0
We have:
Va - Vc = ℰo
Vb - Va = - L di/dt
Vc - Vb = - R i
Therefore:
ℰo - L di/dt - Ri = 0
- L di/dt = Ri - ℰo = R(i - ℰo/R)
We obtain the following differential equation:
di/(i - ℰo/R) = - (R/L )dt
Integrating, we obtain:
i(t) = Const. exp { - (R/L)t} + ℰo/R
Where Const is a constant integration.
We find this constant Const by applying the initial
condition i(0) = 0:
At t = 0, i(0) = 0 = Const + ℰo/R
Thus
Const = - ℰo/R
We define a characteristic time parameter:
τL = L/R called the inductive time constant.
i(t) = - (ℰo/R) exp {- t/τL} + ℰo/R
i(t) = (ℰo/R) (1 - exp {- t/τL})
Instantaneous increasing current through
an inductance: τL = L/R
i(t) = (ℰo/R) (1 - exp {- t/τL})
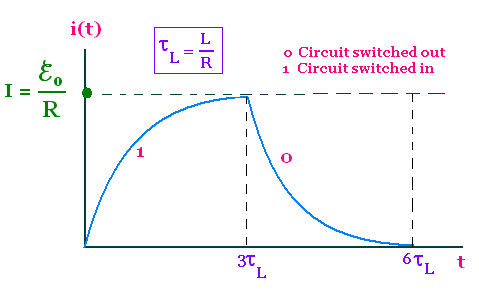
At a long time (t → ∞) i(t) becomes equal to the
steady value I = ℰo/R, that
is the value of the current i without the inductance. The
inductive time constant τL = L/R sets the
time scale for the LR circuit. At t = 5τL, the
value of the current i(t) is already 0.99 ℰo/R.
3.1. Switch at the position 0
At the position 0, the battery is disconnected; the
current decreases during a certain time until it vanishes,
and becomes equal to the steady value I = 0.
At the time t = 0, while the current
has the value io, we disconnect the battery. Thus
the loop rule, with ℰo is :
0 - L di/dt - Ri = 0.
Solving this differential equation, using the initial condition
i(0) = io, gives:
i(t) = ioexp {- t/τL}
Instantaneous decreasing current through
an inductance: τL = L/R
i(t) = ioexp {- t/τL}
At the time t = τL, the current has dropped to
ioexp {- 1} = 0.37io. At t = 3τL,
the current becomes practically zero.
4. Energy transfers in LR circuits
4.1. Energy stored in an inductor
The gravitational potential energy of a mass changes
as the mass moves through a gravitational field.
The electric potential energy of charge carriers changes
as carriers move through a potential difference in a circuit
element.
Consider an inductor, of ohmic resistance r and inductance L.
In addition to the Joule heating in the inductor at
the rate Pr = ri2, there is also
an electric potential energy UL due the self-induced
emf ℰ.
If the current is increasing in the inductor, the self-induced emf
opposing the current is negative, hence the carriers lose potential
energy.
If the current is decreasing in the inductor, the self-induced emf
opposing the current is positive, hence the carriers gain potential
energy.
The potential energy lost by the charge carriers when the current
is increasing is maintained within or stored in the inductor due to
the change in the potential difference between the conductor.
The potential energy gained by the charge carriers when the current
is decreasing is returned or restored or recovered by the inductor due to
the change in the potential difference between the conductor.
Each time the potential energy if transformed to and from
a stored energy in the inductor, called the magnetic energy
of the inductor.
The power P, or rate of energy used or transformed
in the inductor is P = dUL/dt, where dUL is
the infinitesimal electric potential energy change stored
in the inductor. This change dU corresponds to the change di
in current.
We have P = dUL/dt = ℰi = i L (di/dt)
P = Li(di/dt)
Since dUL/dt = i L (di/dt), or
dUL = L i di, we integrate to obtain
UL(t) = (1/2) L i2(t) + const.
At t = 0, UL(t) = 0. Hence const = 0.
Therefore the energy stored in the inductor is:
UL = (1/2) L i2
Energy stored in an inductor:
UL = (1/2) L i2
4.1. Energy stored in an inductor
Consider a solenoid of length l, and cross-sectional area S with
n turns per unit length. Its inductance is: L = μon2Sl.
When crossed by a current I, the produced magnetic field is B = μonI.
Therefore
UL = (1/2) L i2 = (1/2) μon2Sl i2 =
(1/2) μon2Sl (B/μon)2 =
(1/2) Sl B2 (1/μo) = Sl B2/2μo
The product Sl represents the volume of the space inside the solenoid. Hence
the energy density stored in the solenoid is uB = UL/V
= B2/2μo
Energy density stored in the magnetic field of an ideal solenoid:
uB = B2/2μo
This result valid for a solenoid is in fact general.
The energy density of an inductor is equal to the
half of the square of its induced magnetic field
divided by the vacuum permeability.
|
|