Electrostatics:
Effect of the field on a charged particle.

1. Free charged particle in a electric field

We are considering the simplest situation where the electric field is uniform .

In an electric field E, if the only significant force on a charged particle q is the electric force F, then the Coulomb's law and Newton second law together give the expression of the net force:

F = q E = m a or a = q E/m

a is the acceleration of the charged particle of mass m.

1. A charged particle released in a uniform electric field E will be accelerated a long the electric field.

At the origin, we place the release point and orient the field parallel to the x-axis.

The kinematics of the particle released from rest (v_o = 0), like a free-fall particle, is:

a_x = q E/m

x = (1/2)a_xt² = (1/2)(qE/m)t²
v_x = a_xt = (qE/m)t

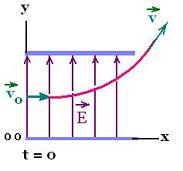
2. Projectile charged particle in a electric field

Now if the positive charged particle enters the field E oriented along the y-axis, perpendicularly with an initial velocity v_o at t = 0, like a projectile, its kinematics equations are:



a_x = 0
a_y = qE/m
x = v_ot
v_x = v_o
v_y = a_yt = (qE/m)t
x = v_ot
y = (1/2) ayt² = (1/2) (qE/m)t² =
(1/2) (qE/m)(x/v_o)² = (1/2) (qE/m)(1/v_o)². x²

That is the particle follows the parabolic path.