Sources of the magnetic field
Oersted discovered in 1819 that a compass needle was deflected
near a conducting wire carrying a current. The electric current was
the source of the magnetic field that exerted a torque on the
compass needle. This observation was the first indication of the
connection between electricity and magnetism.
In this section, we will give the Biot-Savart law and
Ampere's law and some applications of them.
1. The biot-Savart law
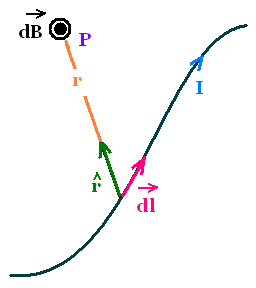
The discovery of Oersted was followed by the experiments by
Amp�re and by Biot and Savart that led to their laws.
In a point in space, the Boit-Savart law determines the magnetic field
due to a distribution of electric currents.
Let's consider a current distribution where the
current element Idl (source of dB) produces the infinitesimal
contribution dB to the magnetic field at the point P
distant of r from the origin of the vector current element dl
(point source).
The direction of the vector dB is given by the direction of
the cross product Idl x r. It is directed out of the page
toward us ⊙. It is perpendicular to both dl and ^r, that is
to the plane formed by Idl and ^r. The sense of the vector db is
given by the right-hand rule.
^r is the unit vector pointing from the current element to the point P.
The Bio-Savart law for an infinitesimal current element is:
| |
|
|
|
→ ^ |
| → |
|
μo |
|
Idl x r |
| dB |
= |
|
|
|
| |
|
4π |
|
r2 |
Integrated along the line of the current distribution,
Biot-Savart law in its integral form is:
| |
|
|
|
→ ^ |
| → |
|
μo |
|
Idl x r |
| B |
= ∫ |
|
|
|
| |
|
4π |
|
r2 |
The magnetic field at a point is the linear superposition 0f the
vector contributions due to each of the infinitesimal current elements.
The constant μo is called the permeability constant
for vacuum. Its value in the SI units is given by:
μo/4π = 1.00 x 10- 7 T.m/A
2. Magnetic field and Electric field analogy
For electromagnetism, the Biot-Savart law is analogous to
Coulomb's law for electrostatics. Coulomb's law gives the
electric field produced by a distribution of charges. If
dq is a differential of infinitesimal element of charge, then
the electric field dE produced at a point P by that charge is
given by the equation:
r is the distance from the element of charge to the point P and
^r is the unit vector directed from the charge to the point P. Integrating
over the charge distribution gives the electric field at the point P:
| |
|
|
|
|
^ |
| → |
|
1 |
|
dq |
r |
| E |
= |
|
∫ |
|
|
| |
|
4π εo |
|
r2 |
|
Now, a current distribution with a current element Idl
produces a contribution dB to the magnetic field at a point P.
r is the distance from the current element(source) to point P.
The Boit-Savart law for a differential current element is:
| |
|
|
|
→ ^ |
| → |
|
μo |
|
Idl x r |
| dB |
= |
|
|
|
| |
|
4π |
|
r2 |
Integrated along the line of the current distribution,
Biot-Savart law in its integral form is:
| |
|
|
|
→ ^ |
| → |
|
μo |
|
Idl x r |
| B |
= |
|
∫ |
|
| |
|
4π |
|
r2 |
The direction of E is radial with respect to the charge dq while
the direction of B is perpendicular to the plane formed by the
vector dl and the the vector r.
3. Magnetic field due to a current
in a long
straight wire
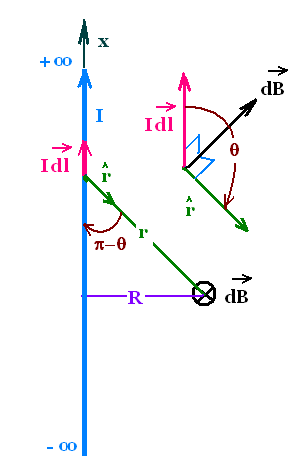
We want to determine the magnetic field produced by
a long straight wire crossed by a current I, where the point P
is in the x-axis and at a perpendicular distance from the wire.
The direction of dB is given by the right-hand rule, so it is
directed into the page. The magnitude of dB is:
dB = (μo/4π) I dx sin θ /r2
sin θ = sin (π - θ) = R/r =
R/[x2 + R2]1/2
dB = (μo/4π) I dx R /r3 =
(μoIR/4π) dx /[x2 + R2]3/2
Therefore
B = (μoIR/4π) ∫ dx /[x2 + R2]3/2
-∞ → + ∞
= (2μoIR/4π) ∫ dx /[x2 + R2]3/2
0 → + ∞
I = ∫ dx /[x2 + R2]3/2
Let x = R tan z. So
dx = R (1 + tg2z) dz =
R (1 + (x/R2) dz
I = ∫ dz R (1 + (x/R2)
/[(x/R)2 + 1]3/2R3 =
(1/R2) ∫ dz/[tan2z + 1]1/2 =
(1/R2) ∫ cos z dz =
sin z + const.
sin z = sin (Arctg(x/R))
Arctg(x/R) = α → x/R = tan α
We have α = θ - π/2. Hence
sin z = sin (θ - π/2) = - cos θ =
cos(π - θ) =
x/r =
x/[x2 + R2]1/2
Therefore
I = (1/R2) . x/[x2 + R2]1/2 =
(1/R2)(1 - 0) = (1/R2)
0 → + ∞
B = (2μoIR/4π) . (1/R2)
B = (μoI/2πR)
Magnetic field due to a current in a long straight wire :
B = (μoI/2πR)
4. Magnetic field due to a current loop
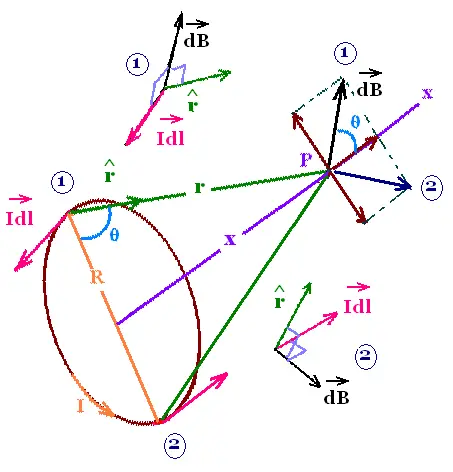
Consider the magnetic field produced by a circular loop
of radius R carrying a current I. We want to determine
the magnetic field on a point P along the axis of the loop,
x-axis. Any point on the loop is equidistant to that point P.
That is for a given point P on the x-axis, then a given
distance x, r remains constant. The contribution dB to the
field at this point is:
dB = (μo/4π) Idl/r2 that we resolve
into the components parallel and perpendicular to the x-axis.
From symmetry, the pependicular components add to zero. The
parallel components give :
dB∥ = (μo/4π) Idl cos θ/r2
= (μo/4π) Idl/r2 . (R/r) =
(μo/4π) IRdl/r3
Therefore
B = ∫dB dl = (μo/4π) IR/r3 ∫ dl =
(μo/4π) IR/r3 (2πR) =
(μo/2) IR2/r3
= (μoIR2)/2r3
Magnetic field on the axis of a current loop:
B = (μoIR2)/(x2+R2)3/2
|