Mutual inductance

Mutual inductance

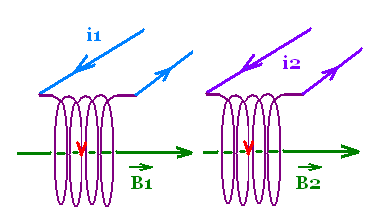
Consider two coils 1 and 2 one in front of the other, of length l1 and l2, cross-sectional areas S1 and S2, with n1, and n2 turns per unit length each.

The two coils carry the currents i1 and i2, . The current i1 produces a magnetic field B1 inside the coil 1 that influences the nearby coil 2.

When i1 changes (then B1 changes), it produces in the coil 1 a self-induced emf = ℰ₁₁, and a induced emf = ℰ₂₁ in the coil 2 through (external field) B1.

Similarly, the current i2 produces a magnetic field B2 inside the coil 2 that influences the nearby coil 1.

when i2 changes in the coil 2 (then B2 changes), it produces in the coil 2 a self-induced emf = ℰ₂₂, and a induced emf = ℰ₁₂ in the coil 1 through (external field) B2.

The effect of inducing an emf by one coil on the other is called mutual induction.

Self-induction in the coil 1
The magnetic field inside is B1 = μ_o n1 i1
The magnetic flux due to B1 that links this coil is Φ₁₁ = B1 S1
Its emf = ℰ₁ = - n1 dΦ_B1/dt
= - μ_on1² S1 l1 di1/dt
Its self-inductance is L1 = μ_on1²S1l1

Self-induction in the coil 2
The magnetic field inside is B2 = μ_o n2 i2
The magnetic flux due to B2 that links this coil is Φ₂₂ = B2 S2
Its self = ℰ₂ = - n2 dΦ_B2/dt
= - μ_on2² S2 l2 di2/dt
Its self-inductance is L12 = μ_on2²S2l2

Interaction: Mutual-induction of the coil 1 and the coil 2

The magnetic field inside the two coils is B1 + B2 = μ_o n2 i2 + μ_o n1 i1

The magnetic flux due to (B1 + B2) that links this coil 1 is Φ_1-12 = (B1 + B2) S1
and the magnetic flux due to (B1 + B2) that links this coil 2 is Φ_2-12 = (B1 + B2) S2

The emf of the coil 1 is emf = ℰ₁₂
= - n1 l1 dΦ_{(B1 + B2)}/dt
= - n1 l1 S1 μ_o d(n2 i2 + n1 i1)/dt
= - n1 l1 S1 μ_o (n2 di2/dt + n1 di1/dt)

The emf of the coil 2 is emf = ℰ₂₁
= - n2 l2 dΦ_{(B1 + B2)}/dt
= - n12 l2 S2 μ_o d(n2 i2 + n1 i1)/dt


We define:

The mutual-inductance for the coil 1:
ℰ₁₂ = - M12 di1/dt, and
The mutual-inductance for the coil 2:
ℰ₂₁ = - M21 di2/dt, and

M12 and M21 are called coefficient of mutual inductance. They depend on the geometrical factors of the coils.

We can consider the particular case where M12 = M21 = M. M is then the inductance of the pair. The SI unit of the mutual inductance is the Henry.