Relativity: Contravariant and covariant transforms

1. Lorentz Transformations Matrices

From the reference frame at rest (RF):
The velocity of the reference frame (RF) is 0
The velocity of the moving reference frame (MF) is v
The velocity of the moving object is u.

From the moving frame (MF):
The velocity of the moving reference frame (MF) is 0
The velocity of the reference frame (RF) is - v
The velocity of the moving object is u'


In the (MF):, Lorentz Transformations give:



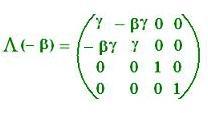
ct' = γ(ct - βx)
x' = γ(x - β ct)
y' = y
z' = z

The contravariant 4-Vector V'(ct',x',y',z') is the transformed of he contravariant 4-Vector V(ct,x,y,z) by:

V' = Λ(- β) V

In the (RF), Lorentz Transformations give:


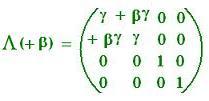
ct = γ(ct' + βx')
x = γ(x' + β ct')
y = y'
z = z'

The covariant 4-Vector V(ct,x,y,z) is the transformed of he covariant 4-Vector V(ct',x',y',z') by:

V = Λ(+β) V'

where
γ = 1/[1 - β²]^1/2, and β = v/c

2. Contravariant Lorentz transformation

We have:
ct' = γ(ct - βx)
x' = γ(x - β ct)
y' = y
z' = z

Taking partial derivatives gives:

Therefore, the components of the matrix Λ(-β) are:

Λ(-β)₀₀ = γ = ∂(ct')/∂(ct)
Λ(-β)₀₁ = - γ β = ∂(ct')/∂(x)


Λ(-β)₁₀ = - γ β = ∂(x')/∂(ct)
Λ(-β)₁₁ = γ = ∂(x')/∂(x)

Λ(-β)₂₂ = γ = ∂(y')/∂(y)
Λ(-β)₃₃ = γ = ∂(z')/∂(z)
...
The others are zero.

If we denote by xⁱ the contravariant components of V(ct,x,y,z) and by yⁱ the contravariant component of V'(ct',x',y',z'), we can write the components of the matrix Λ(-β) as the following:

Λ(-β)_ij = ∂(yⁱ)/∂(x^j)

i = 0,1,2,3 stands for line and j = 0,1,2,3 stands for column.

Therefore:
y⁰ = ΣΛ(-β)_0j x⁰
y¹ = ΣΛ(-β)_1j x¹
y² = ΣΛ(-β)_2j x²
y³ = ΣΛ(-β)_3j x³


or:
yⁱ = ΣΛ(-β)_ij xⁱ = Σ ∂(yⁱ)/∂(x^j) xⁱ
or
V'ⁱ = Σ ∂(yⁱ)/∂(x^j) Vⁱ

or
Vⁱ(in the frame y) = Σ ∂(yⁱ)/∂(x^j) Vⁱ(in the frame x)

Vⁱ(y) = Σ ∂(yⁱ)/∂(x^j) Vⁱ(x)

Using the Einstein summation convention (not writing the symbol Σ), we can write

V^μ(y) = (∂y^μ/∂x^ν) V^ν(x)

3. Covariant Lorentz transformation

WE have:
ct = γ(ct' + βx')
x = γ(x' + β ct')
y = y'
z = z'

Taking partial derivatives gives:

Therefore, the components of the matrix Λ(+β) are:

Λ(+β)⁰⁰ = γ = ∂(ct)/∂(ct')
Λ(+β)⁰¹ = γ β = ∂(ct)/∂(x')


Λ(+β)¹⁰ = γ β = ∂(x)/∂(ct') Λ(+β)¹¹ = γ = ∂(x)/∂(x')

Λ(+β)²² = γ = ∂(y)/∂(y')
Λ(+β)³³ = γ = ∂(z)/∂(z')
...
The others are zero.

If we denote by x_i the covariant components of V(ct,x,y,z) and by y_i the contravariant component of V'(ct',x',y',z'), we can write the components of the matrix Λ(+β) as the following:

Λ(+β)^ij = ∂(x_i)/∂(y_j)

i = 0,1,2,3 stands for line and j = 0,1,2,3 stands for column.

Therefore:
x₀ = ΣΛ(+β)^0j y₀
x₁ = ΣΛ(+β)^1j y₁
x₂ = ΣΛ(+β)^2j y₂
x₃ = ΣΛ(+β)^3j y₃


or:
x_i = ΣΛ(+β)^ij x_i = Σ ∂(x_i)/∂(y_j) x_i
or
V'_i = Σ ∂(x_i)/∂(y_j) V_i

or
V_i(in the frame x) = Σ ∂(x_i)/∂(y_j) V_i(in the frame y)

V_i(x) = Σ ∂(x_i)/∂(y_j) V_i(y)

Using the Einstein summation convention (not writing the symbol Σ), we can write:


V_μ(x) = ∂(x_μ/∂y_ν) V_ν(y)

4. Contravariant and covariant transform: General case

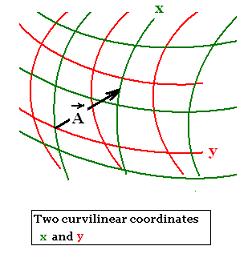
If a vector A(x) has the contravariant components x^μ in the curvilinear reference frame "x", its transformed contravariant vector A(y) in the curvilinear reference frame "y" has the components y^ν.

If A(x) is a scalar such as temperature, its related magnitude remains the same A(x) = A(y)

If A(x) is a vector, a little displacement dA(x) of A(x) in the coordinate reference frame "x" involves its related transformed displacement dA(y) of the transformed A(y) in the coordinate reference frame "y".

That is the displacements of the components dx^μof dA(x) in the coordinate reference frame "x" involve dy^ν in the coordinate reference frame "y".

We can write the following total differential:
dA(x) = Σ (^ν) (∂ A(x)/∂x^μ) dx^ν =
(∂ A(x)/∂x^μ) dx^ν

and

dA(y) = Σ (^ν) (∂ A(y)/∂y^μ) dx^ν =
(∂ A(y)/∂y^μ) dy^ν

The transformed contravariant components of dA(y) are:
dy^μ = Σ(^ν)(∂ y^μ)/∂x^ν) dx^ν =
(∂ y^μ)/∂x^ν) dx^ν

The transformed contravariant components of A(y) are:
y^μ = Σ(^ν)(∂ y^μ)/∂x^ν) x^ν =
(∂ y^μ)/∂x^ν) x^ν

Therefore:
The transformed contravariant vector A^μ(y) is written as:
A^μ(y) = (∂ y^μ)/∂x^ν) A^ν(x)

Similarly;
The transformed covariant vector A_ν(x) is written as:
A_ν(x) = (∂ x_ν)/∂y_μ) A_μ(y)

A^μ(y) = (∂y^μ/∂x^ν) A^ν(x)

A_ν(x) = (∂x_ν/∂y_μ) A_μ(y)