General Relativity
© The scientific sentence. 2010
| Relativity: Newtonian gravitational field
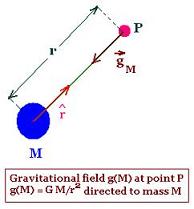
1. Gravitational field of single mass
The weight of an object is the gravitational force of the
the earth acting on it. More generally, the gravitational force
F acting on an object of mass m, located at a point P, is due to the
gravitational field g of another mass M.
The law of universal gravitation is:
F = - G m M r/r2
G is the gravitational constant, r is the distance between the two
masses, and the unit vector r is directed from M to m. The
force F is directed from m to M.
Therefore, we write:
g = G M /r2
So
F = - g m r
F = - g m r
The gravitational force acting on a particle is equal to its mass times
the gravitational field created by another mass.
Hence the gravitational field g has then the following expression:
(notice that rr = 1)
g = - (F/m)r = - (G M/r2) r
g = - (F/m)r = - (G M/r2) r
The gravitational field is the the gravitational force per unit
of mass. It is function of the distance (latitude for earth) and
mass of the field.
We have used the definition of g as the acceleration of an object
due to the gravity of the earth of magnitude near the earth surface is
- 9.80 m/s2. The sign minus is set because
the unit vector is directed from the center of the earth and the
acceleration is downward.
2. Gravitational field of many masses
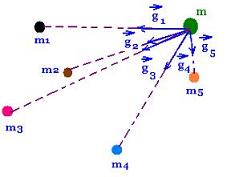
For many masses m1, m2, m3, ..., mn of gravitational fields
g1, g2, g3, ..., gn resprctively, the mass m undergoes a unique
resultant net gravitational field g wich is:
g = - (G m1/r12) r1 - (G m2/r22) r2 - (G m3/r32) r3
... - (G mn/rn2) rn
= - G Σ (mi/ri2) ri
g = - G Σ (mi/ri2) ri
3. Gravitational Gauss's law
3.1. single mass
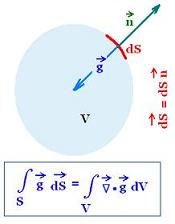
Gauss's law is written for the gravitational field vector as:
∫s g . dS = ∫v ∇. g dV
At spherical distance r, we have g = g(r).
With g = - G m/r2 r, and
g . dS = g dS n . r = g dS
Gauss's theorem becomes:
∫(s) g . dS = 4 π r2 g(r)
= - G m/r2 x 4 π r2 = - 4 πG m
Single mass
∫s ∇. g = - 4 πGm
3.2. Many masses inside a spherical contour S
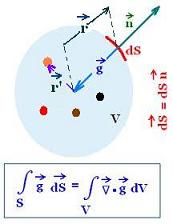
m = Σ mi = ∫ dm
dm = ρ dV = ρ(r') d3r'
Gauss's theorem becomes:
∫v ∇ g dV = - 4 πG ∫v ρ dV
∫v∇ g dV = ∫v(- 4 πG ρ) dV
Therefore
∇ g = - 4 πG ρ
Many masses
∇. g = - 4 πGρ
3.3. Poisson's equation for gravity
Notice that by definition:
An acceleration field A(r) is equal to the negative derivative of its
gravitational potential - ∂Φ/∂r
The Newtoniam (classical) accelerartion
field g is:
g = g(r) = F/m = (GMm/r2)/m = GM/r2 =
- ∂Φ/∂r,
where Φ = - GM/r is the
Newtonian gravitational potential.
Its gradient has the expression:
∇. g = - 4 πGρ
The gravitational field g = g(r) is a vector, so is
- ∂Φ/∂r.
We can then write:
g = - (∂Φ/∂r) er.
With del or
gradient operator, it can be written:
g = - ∇Φ
Therefore:
∇. g = ∇.(- ∇Φ) = - ∇2Φ
That is:
- 4 πGρ = - ∇2Φ
or
∇2Φ = 4 πGρ
∇2Φ = 4 πGρ
That is Poisson's equation for gravity.
|
|