General Relativity
© The scientific sentence. 2010
| Relativity: Metrics & tangent vectors
In differential geometry, a metric is a function that describes
the distances between pairs of points in a space or space-time.
2. Basis gμ of tangent vectors
x = (x0, x1, x2, x3)
y = (y0, y1, y2, y3)
dx = (dx0, dx1, dx2, dx3)
dy = (dy0, dy1, dy2, dy3)
dy0 = (∂y0 /∂x0)dx0 + (∂y0 /∂x1) dx1
+ (∂y0 /∂x2)dx2 + (∂y0 /∂x3)dx3 = (∂y0 /∂xν)dxν
ν = 0. 1. 2. 3.
Similarly
dy1 = (∂y1 /∂xν)dxν
...
dyμ = (∂yμ /∂xν)dxν
vector g0 = ∂/∂0 (vector dy)
vector g1 = ∂/∂1 (vector dy)
...
vector gμ = ∂/∂μ (vector dy)
or
vector gμ = ∂dym /∂μ
dym are all the components of the vecto dy.
Now
The scalar product of the two vectors
gμ and gν is:
vector gμ . vector gν =
∂dym /∂μ
∂dyn /∂ν
Therefore:
ds2 = dy dy =
dym dyn = gμ dxμ
gν dxν =
gμ . gν dxμ dxν
ds2 = gμ . gν dxμ dxν
We have already defined the squared line element ds2 as:
if
dym = (∂ym /∂xμ)dxμ, and
dyn = (∂yn /∂xν)dxν
then ds2 is defined as:
ds2 = η dym dyn
ds2 = η dym dyn =
ηmn ∂ym /∂xμ)dxμ
(∂yn /∂xν)dxν =
ηmn (∂ym /∂xμ)
(∂yn /∂xν) dxμdxν
with
gμν = ηmn (∂ym /∂xμ)
(∂yn /∂xν)
gμν = ηmn (∂ym /∂xμ)
(∂yn /∂xν)
Therefore
ds2 = gμν dxμdxν
Equating gives:
ds2 = gμ . gν dxμ dxν =
gμν dxμdxν
That is:
gμν = gμ . gν
gμν = gμ . gν
2. Raising & lowering indeces
Lorentz Transformations give:
y0 = γ(x0 - βx1 )
y1 = γ(x1 - β x0 )
y2 = x2
y3 = x3
x0 = γ(y0 + βy1/sup> )
x1 = γ(y1 + β y0 )
x2 = y2
x3 = y3
Let's write the vector A with its contravaiant components:
Aμ = (y0,y1, y2, y3) =
(∂ym/∂xμ) xμ
With its covaiant components, we have:
Aμ = (y0,y1, y2, y3) =
(∂xm/∂yμ) xμ
In the Lorentz transforms: the (∂xm/∂yμ)
factors give the same result as the contravariant factors
(∂ym/∂xμ),
except - β changes int + β. Therefore:
y0 = γ(x0 + βx1 )
y1 = γ(x1 + β x0 )
y2 = x2
y3 = x3
What is the relationship between Aμ and Aμ?
Changing x0 into - x0, and letting
the others the same, we can write the above transformations as:
y0 = - γ( x0 - βx1 ) = - y0
y1 = γ(x1 - β x0 )= y1
y2 = x2 = y2
y3 = x3 = y3
Therefore:
Aμ = gμν Aμ with
xμ = gμν xμ
gμν is the the following tensor metric:
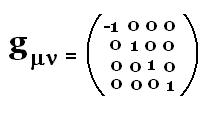
Aμ = gμν Aμ with
xμ = gμν xμ
Raising indices:
Aμ = gμν Aν
with
xμ = gμν xν
We can remark gμν = gμν-1
gμν-1 is the inverse of gμν . We write
gμν-1 = gνμ
gμν-1 = gμν
so
gμν = gνμ
gμν = gνμ
Lowering indices:
Aμ = gμν Aν
with
xμ = gμν xν
|
|