General Relativity
© The scientific sentence. 2010
|
Gravitational radiation shift
1. Principle of Equivalence
Experiments performed in a uniformly accelerating reference
frame with acceleration a are indistinguishable from the same
experiments performed in a non-accelerating reference frame
which is situated in a gravitational field where the
acceleration of gravity = g = a = intensity of gravity field.
The same experiments are indistinguishable from each other
if they are performed in two reference frames: the first is
a uniformly accelerated with acceleration a, and the second is
not accelerated but present an accelerated field with the
same acceleration a.
Thus if we measure the frequency ν of a photon in an
accelerating reference frame where the acceleration is a,
the same value will find in a non-accelerated frame present
in a gravitational where the acceleration of gravity = g = a.
Therefore if we are in a non-accelerating reference (or inertial) frame
within the gravitational field, the frequency of an accelerating
source of photon will be shifted as it is in the Doppler effect
We want then to measure the shift in radiation frequency
related to the relativistic Doppler shift due to an accelerating
light source, by the gravitational field.
2. Relativistic Doppler effect
Moving source toward an observer at rest
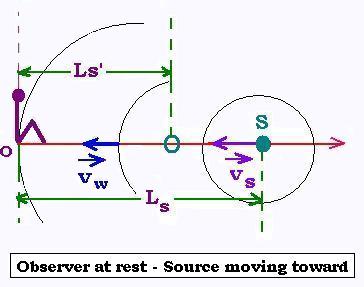
2.1. Doppler effect
The observer is at rest and the source
S is moving at a speed Vs toward this observer. The wave propagates
at the speed Vwin all directions and toward the observer of course.
When this observer receives a wavefront, at this precise time, the
source is not located at the distance Ls but at L's. For the observer, the
period of the wave is T's. And at this precise time, the wave has
travelled Ls = Vw. T , where T is the real period.
T's is the apparent period.
We can write:
L's = Ls - Vs . T
Because Ls = Vw. T
and L's = Vw. T's
Thus :
Vw. T's = Vw. T - Vs . T = (Vw- Vs) . T
Or:
1/T's = Vw/(Vw- Vs) (1/T)
ƒ' = Vw/(Vw- Vs) ƒ
ƒobs = ƒ . Vw/(Vw- Vs)
ƒobs is the apparent frequency.
2.2. Relativistic Doppler effect
In the case of a photon
Vw = c ,
and a source moving at speed
Vs = v
We have:
ƒobs = ƒ . c/(c - v)
In the relativistic case:
ƒrel-obs = �obs /γ
Where
γ = (1 - v²/c²)-1/2
Therefore
ƒrel-obs = ƒ(1 + v/c) = ƒ(1 + at/c)
3. Gravitational radiation shift
The acceleration is g, so v = gt and t = h/c.
h is the length of the photon's path in the time t. Hence
ƒrel-obs = ƒ(1 + gh/c²), or
c/ƒrel-obs = c/ƒ(1 + gh/c²)
λrel-obs = λ/(1 + gh/c²)
The equation in terms of wavelengths is written as:
λrel-obs = λ/(1 + gh/c²)
In terms of frequencies, we have:
ƒrel-obs = ƒ(1 + gh/c²)
or
ƒrel-obs - ƒ = ƒ. gh/c²
That is
(ƒrel-obs - ƒ)/ƒ = gh/c²
The relative gravitational radiation shift is:
(ƒrel-obs - ƒ)/ƒ = gh/c²
Since the frequency is reduced, this effect is called the
gravitational red shift or the Einstein red shift.
In 1 km, with g = 9.8 m/s² and c = 3 x 108 m/s,
the related relative gravitational radiation shift is about
10- 11 %.
4. Gravitational radiation shift and Schwarzschild radius
This shift is due to a lost of energy for the photon. If we attribute
a mass m for the photon of initial energy hνo and final
energy at the height hν, we can write:
hν = hνo + potential energy
This potential energy can be written as:
PE = - G m M/r
G is the gravitational constant
m mass of photon
M mass of sphere of gravity (earth)
r the height (position) where the photon has the energy hν
Therefore
hν = hνo - G m M /r
The total energy of the photon having the mass m is:
hνo = mc2.
Hence
m = hνo/c2.
The expression of the potential energy becomes:
PE = - G m M /r = - G M hνo/r c2
PE = - G m M /r = - G M hνo/r c2
The above equation becomes:
hν = hνo - G M hνo/r c2 =
hνo[1 - G M /r c2]
Or
[hν - hνo]/hνo = - G M /r c2
(ν - νo)/νo = - G M /r c2
This result shows that the frequency is reduced.
Recall that the Schwarzschild radius rs is:
rs = 2GM/c2
Which also equal to the escape speed of the photon.
(ν - νo)/νo = - G M /r c2 =
- rs/2r
(ν - νo)/νo = - rs/2r
The Earth's Schwarzschild radius is about 9.0 mm, so:
- rs/2r = - 1 at r = rs/2 = 4.5 mm. In this
conditions:
(ν - νo)/νo = - 1. That is ν = 0.
That is a photon traveling 4.5 mm in the earth gravitational field
will disappear. It does make any sense!.
|
|