1. Similar and congruent triangles

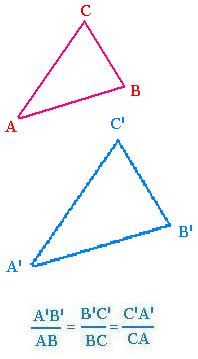
Two objects are similar if they both have the same shape.

Two triangles &eElta;ABC and ΔA'B'C'are similar (ΔABC &simi; ΔA'B'C') if the following proportionality is satisfied:

A'B'/AB = B'C'/BC = C'A'/CA

They are congruent (ΔABC ≅ ΔA'B'C') if they are similar and have the same size. The above ratio is then equal to 1.

There are two rules for similar triangles:

1. The AA (Angle-Angle) rule:

If two angles of a triangle are equal to two angles of another
triangle, then the triangles are similar ( in a triangle, if
two angles are known, the third is obviously as the supplement).
If the angles are equals:
∠A = ∠A', ∠B = ∠B', and ∠C = ∠C'. According to the sine law, we write:
For the ΔABC:
AB/sin C = BC/sin A = AC/sin B, that gives:

sin A/sin C = BC/AB    (I.1)
sin B/sin A = AC/BC    (I.2)
sin B/sin C = AC/AB    (I.3)

For the ΔA'B'C':
A'B'/sin C' = B'C'/sin A' = A'C'/sin B'=
A'B'/sin C = B'C'/sin A = A'C'/sin B; that gives:

sin A/sin C = B'C'/A'B'    (II.1)
sin B/sin A = A'C'/B'C'    (II.2)
sin B/sin C = A'C'/A'B'    (II.3)

The two group relationships (I) and (II) gives:
BC/AB = B'C'/A'B'
AC/BC = A'C'/B'C'
AC/AB = A'C'/A'B'

Then:
A'B'/AB = B'C'/BC = A'C/AC, that is the ΔABC and the ΔA'B'C' are similar.

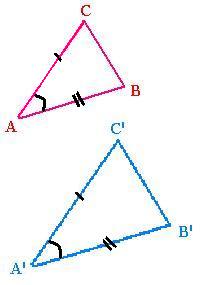2. SAS (Side Angle Side) rule:

If two sides of a trinagle, including an angle, are proportional to those of another trinagle including an angle equal to the first; then these two triangles are similar.

Let the angle ∠A = ∠A', and the sides AC = m A'C' and AB = m A'B' ( m is the related coefficient of proportionality). According to the Cosine Law, we write:

For the ΔABC:
BC² = AC² + AB² - AC . AB cos A, that is:

For the ΔA'B'C':
B'C'² = A'C'² + A'B'² - A'C' . A'B' cos A', that is:
B'C'² = m² AC² + m² AB² - m² AC . AB cos A
which is equal to m² BC²
Then B'C' = m BC

The three sizes are then proportional:
m = B'C'/BC = A'B'/AB = A'C'/AC

The triangles ΔABC and ΔA'B'C' are similar.

To recap:
SSS (proportionality) → similar triangles
AA (or AAA) → similar triangles
SAS → similar triangles

2. Applications

2.1. Tangent and secant

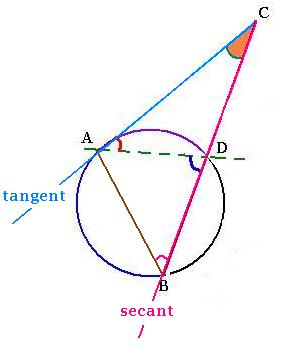
The angle ∠CAD = arc AD/2, so the angle ∠B is. Then ∠ CAD = ∠ABC. The angle ∠C is common. We have then the case of AA or AAA rule, furthermore the triangles ΔABC and ΔADC are similar.
Then:
BC/AC = AC/CD = AB/AD. Thus:
AC² = CD . CB

CA² = CD . CB

2.2. Relationships in the rectangular triangle

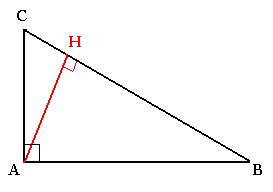
Let's draw a rectangular triangle CAB, where the angle A is right.The point H is the projection of the point A on the the side BC. The angle AHC and the angke AHB are right. For the triangles CAB and AHB, the angle B is common. Then the angles BAH and ACH are equal: BAH = ACH. The triangles AHB and CAB are then similar. Thus:
BC/AB = AC/AH = AB/BH     (1)

Similarly, the angle C is common, the angles CAH and ABC are equal: CAH = ABC. The triangles CHA and CAB are then similar. Thus:
BC/AC = AC/CH = AB/AH     (2)
The triangles CHA, AHB and CAB are then similar. Using the similarity of the triangles CHA and AHB, we can write:
AB/AC = AH/CH = HB/AH     (3).

The relationships (1), (2) and (3) give successively:
AB² = BH . BC
AC² = BC . HC
AH² = BH . CH

2.3. Congruent angles

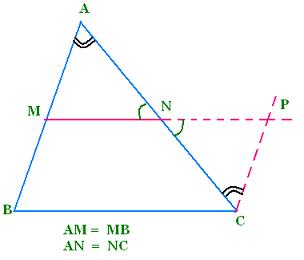
In the triangle ABC, we join the middle point M of the size AB to the middle point N of the size CA. We want to prove that MN is parallel to BC and equal to its half.

Hypothesis: MA = MB and NA = NC
Conclusion: MN//BC and MN = BC/2

Let's extend MN to MP and draw the parallel CP to the side AB. The side AC as a secant gives:
Angle CAB = angle ACP (as alternate interior angles). The two angles ∠CNP and ∠MNA are vertical and then congruent. Then ∠CPN = ∠AMN. Furthermore the triangles ΔAMN and ΔCNP are similar. More, they are congruent (the ratio AN/NC = 1).

The angles CNP and MNA are congruent, then PC = AM = MB ( by hypothesis), then MB = CP and ABCP is a parallelogram ( because if CP // MB and CP = BM, then the quadrilateral MBCP is a parallelogram), then MN//BC.

MBCP is a parallelogram, then MP = BC. Since NP = MN, then the point N is the middle of MP, and MP = 2 MN
2MN = MP = BC, then MN = BC/2

conclusion:
MN // BC and MN = BC/2