Mathématiques 45: Algèbre:
Systèmes d'inéquations
1. Inéquations:
1.1. Règle:
Pour étudier une inéquation du premier degré,
on effectue les étapes suivantes:
1. On la ramène à sa forme fonctionnelle.
C'est à dire de la forme:
y > a x + b
2. On ecrit son équation correspondante:
y = a x + b
3. On fait une table de valeur pour cette
équation.
4. On trace sa droite sur un plan
cartésien. Cette droite s’appelle la
droite frontière souvent représentée
en pointillé.
. On prend un point quelconque P(xo, yo)
du plan et on teste s'il vérifie
l'inéquation.
yo > a xo + b ?
. Si oui, le demi-plan où il se trouve est
le domaine des solutions.
Si non, le demi-plan où il ne se trouve pas
est le domaine des solutions.
1.2. Exemple:
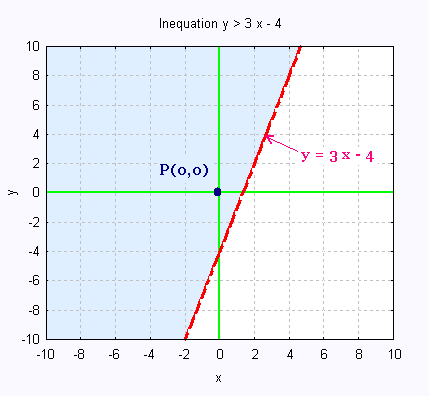
Colorier sur un graphe l'ensemble des
solutions de l'inéquation
y > 3 x - 4
.
On prend le P(0, 0) qui réussit le
teste:
0 > (3) (0) - 4 ? ou
0 > - 4 ? OUI.
Ainsi le demi-plan qui contient le
point P(0, 0) contient toutes les
solutions de l'inéquation.
2. Systèmes d'inéquations:
2.1. Règle:
On applique la même méthode pour chaque inéquation.
L'ensemble des solutions est égal à l'intersection
des deux demi-plans solutions de chaque inéquation.
2.2. Exemple:
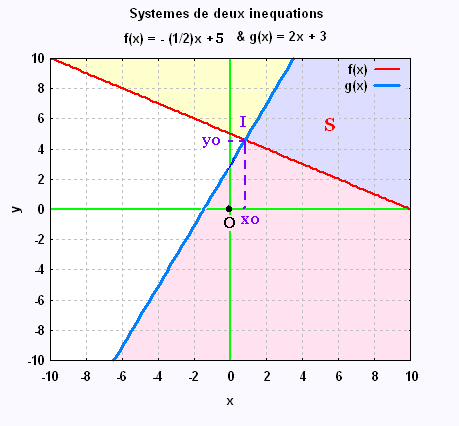
On considère deux droites définies par leurs inéquations
suivantes:
y > - (1/2) x + 5
y ≤ 2 x + 3
Colorier sur un graphe l'ensemble S des
solutions du système des deux inéquations.
On prend le O(0, 0) comme point-teste:
Nous avons:
1. y > - (1/2) x + 5
0 > - (1/2) (0) + 2 ? ou 0 > 2 ? NON.
Ainsi (0,0) n'appartient pas au demi-plan solution de
cette inéquation.
Le demi-plan supérieur (jaune) est l'ensembe des
soltions de cette inéquation.
2. y ≤ 2 x + 3
0 ≤ - (1/2) (0) + 2 ? ou 0 ≤ 2 ? OUI.
Ainsi (0,0) appartient au demi-plan solution de
cette inéquation.
Le demi-plan de droite (rouge) est l'ensembe des
soltions de cette inéquation.
3. Système d'inéquations
L'ensemble total S des solutions est égal
à l'intersection des deux demi-plans
solutions de chaque inéquation.
Les points pris dans S vérifient à la fois
l'inéquation y > - (1/2) x + 5 et l'inéquation
y ≤ 2 x + 3.
2.3. Ensemble des solutions:
Quelles sont alors les coordonnées xoey
yo du point I d'intersection des deux
droites d'équations y = - (1/2) x + 5 et y = 2 x + 3 ?
On utilise l'une des méthodes de comparaison, d'addition
ou de substitution.
Par exemple, la méthode de comparaison donne:
- (1/2) x + 5 = 2 x + 3 → xo = 4/5 = 0.8
donc yo = 2(4/5) + 3 = 23/5 = 4.6
L'ensemble des abscisses x solutions du système
d'inéquations est:
Sx = ]4/5, + ∞[.
L'ensemble des points solutions du système
d'inéquations est:
SP = {(x,y):∀x>4/5,
y>-(x/2)+5 et y≤2x+3}
|