Mathématiques: Les brevets

Brevet des collèges     Amérique du nord     juin 2004.

Activités numériques

Exercice 1

1.
A = 1/7 + 6/7÷12/35

A = 1/7 + 6/7÷12/35 = 1/7 + 6/7 x 35/12 =
1/7 + 6/7 x 5 x 7/12 = 1/7 + 5/2 = 2/14 + 35/14 =
37/14.

A = 37/14

2.
B = (√17 - 1)(√17 + 1)
C = (3 - √7)²
D = B - C

a) B = (√17 - 1)(√17 + 1) = 17 - 1 = 16.

B= 16

C = (3 - √7)² = 9 - 6√7 + 7 = 16 - 6√7

C = 16 - 6√7

D = B - C = 16 - 16 + 6√7 = 6√7

D = 16√7

Exercice 2

1.
E = (4x + 5)(x - 2) - x(x + 4)
F = (3x - 10)(x + 1)

1.
E = (4x + 5)(x - 2) - x(x + 4) =
4x² - 8x + 5x - 10 - x² - 4x = 3x² - 7x - 10

E = 3x² - 7x - 10

F = (3x - 10)(x + 1) = 3x² + 3x - 10x - 10 =
3x² - 7x - 10

F = 3x² - 7x - 10

On trouve:

E = F

2.
E = 0 est équivalent à F = 0. Donc:

(3x - 10)(x + 1) = 0. D'où: x = - 1 ou x = 10/3

L'ensemble des solutions de l'équation E = 0 est:

S = {- 1, 10/3}

Exercice 3

Deux courses le même jour et à la même boulangerie.
5,85 euros pour 5 pains au chocolat et 3 croissants.
3,65 euros pour 3 pains au chocolat et 2 croissants.

1. Système d’équations traduisant ces données:

Soient:

x le prix d’un pain au chocolat et
y le prix d’un croissant. On a:

$\large\color{brown}{ \begin{cases} 5x + 3y &= 5.85\cr 3x + 2y &= 3.65 \end{cases} }$

2. Par la méthode de comparaison, on trouve:

$\large\color{black}{ \begin{cases} 3y &= 5.85 - 5x \\ 2y &= 3.65 - 3x \end{cases} } \\ \text{ } \\ \text{ ou }\\ \text{ } \\ \\ \\ \large\color{black}{ \begin{cases} y &= (5.85 - 5x)/3\\ y &= (3.65 - 3x)/2 \end{cases} } \\ \text{ } \\ \text{ Donc }\\ \text{ } \\ \eqalign{ (5.85 - 5x)/3 &= (3.65 - 3x)/2 \\ 2(5.85 - 5x) &= 3(3.65 - 3x) \\ 10x - 9x &= 2 \times 5.85 - 3 \times 3.65 \\ x &= 2 \times 5.85 - 3 \times 3.65\\ x &= 0.75 } \qquad \Large\color{blue}{ \eqalign{ x &= 0.75 } } \text{ } \\ \\ \\ \text{ En remplaçant x dans l'une ou l'autre des équations, on trouve:} \\ \text{ } \\ \\ \\ \eqalign{ y &= (5.85 - 5x)/3 \\ &= (5.85 - 5 \times 0.75)/3 \\ y &= 0.7 } \qquad \Large\color{blue}{ \eqalign{ y &= 0.70 } } \text{ } \\ \\ \\ \text{ } \\ \text{ } \\ \large\color{brown}{ \bf\text{ Prix d’un pain au chocolat = 0.75 }\unicode{0x20AC}\text{.} \\ \text{ } \bf\text{Prix d’un croissant = 0.70 }\unicode{0x20AC}\text{.} \\ }$

Exercice 4

On dispose de 126 iris et 210 roses.

En utilisant toutes ses fleurs, on veut réaliser des bouquets contenant tous le même nombre d’iris et le même nombre de roses.

2.
126 = 2 x 3² x 7
210 = 2 x 3 x 5 x 7

1. On ne peut pas réaliser 15 bouquets, parce que 15 n'est pas un diviseur commun de 126 et de 210.

2. On peut réaliser 14 bouquets, parce que 14 est un diviseur commun de 126 et de 210.

3.
a) Le nombre maximal de bouquets que l'on peut réaliser est égal au pgcd de 126 et 210, qui est 2 x 3 x 7 = 42.

b) La composition de chacun des bouquets est 126/42 = 3 iris et 210/42 = 5 roses.

Activités géométriques

Exercice 1

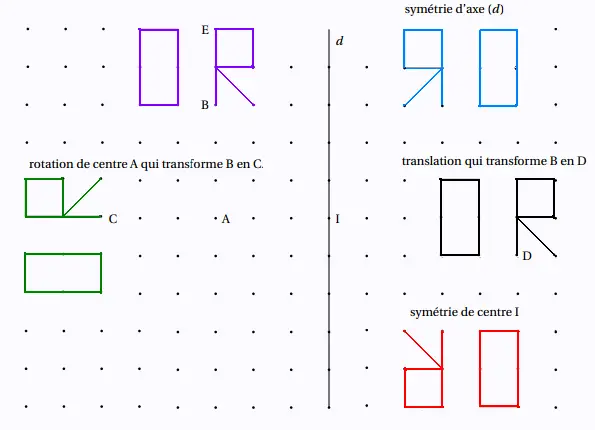
Exercice 2

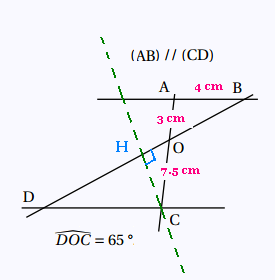
1. Les droites (BD) et (AC) sont sécantes en O. Le droites (AB) et (CD) sont parallèles. Ainsi, d'après le théorème de Thalès: OA/OC = OB/OD = AB/CD.

C'est à dire

3/7.5 = OB/OD = 4/CD

D'où CD = 4 x 7.5/3 = 10

CD = 10 cm.

2. cos (∠DOC) = OH/OC = OH/7.5

Donc OH/7.5 = cos(65°) = 0.4226

OH = 0.4226 x 7.5 = 3.1696.

OH = 3.17 cm.

Exercice 3

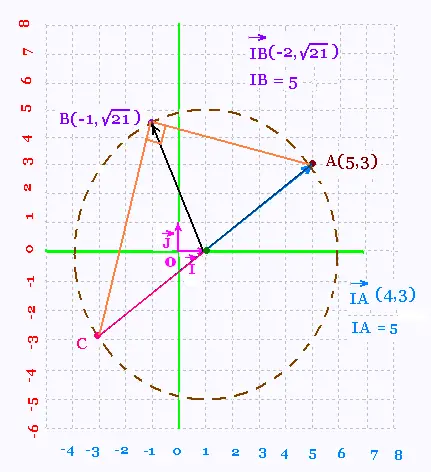
1.
a)

$\text{b) Les coordonnées du vecteur }\overrightarrow{IA} \text{ sont (5 -1, 3 - 0) = (4,3)} \\ \text{ } \\ \\ \text{c) Distance IA = } \sqrt{4^2 + 3^2} \text{ = 5 } \text{ } \\ \text{ Distance IB = } \sqrt{(- 2)^2 + 21} \text{ = 5 } \text{ } \\ \text{ } \\ \color{blue}{\bf\text{2. }} \\ \text{ } \\ \color{green}{\text{a) Les distances IA et IB sont égales à 5. } \\ \text{Elles constituent donc le rayon d'un même cercle de } \\ \text{centre I passant par A et B.}} \text{ } \\ \text{ } \\ \color{blue}{\bf\text{3. }} \\ \text{ } \\ \color{brown}{\text{b) Le segment [AC] est le diamètre du cercle. B est sur le cercle.} \\ \text{ } \\ \text{Donc B est droit. Ainsi le triangle ABC est rectangle en B.}}$

Problème

Partie A

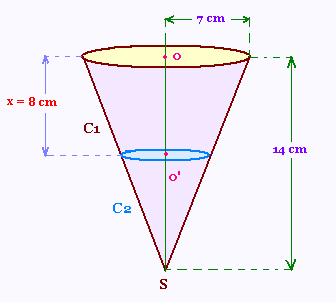
1. Le volume V1 du cône C1 est égal à
(1/3) (aire de la base) x (hauteur) =
(1/3) (π x 7² x (14) = 686 π/3.

V1 = 686 π/3 cm³.

2. Nous avons OO' = 8 cm.

Par un plan parallèle à la base du cône C1 et passant par o', on coupe une section et on obtient une réduction du disque de base. On nome C2 le petit cône obtenu.

Le rayon r1 du cône C1 est parallèle au rayon r2 du cône C2. Les droites latérales est la droite (oo') sont sécantes en S. Le théorème de Thalès permet d'ecrire:

So'/So = r2/r1

D'où r2 = r1 x So'/So = r1 x (So - oo')/So =
7 x (14 - 8)/14 = 7 x 6/14 = 3

r2 = 3 cm

3. Le volume V2 du cône C2 est la réduction du volume V1 de C1:

V2/V1 = (r2/r1)³ = (3/7)³

Donc

V2 = V1 x (3/7)³ = (1/3) (π x 7² x (14) x (3/7)³ =
π x (2) x (3² = 18 π

V2 = 18 π cm³ .

4. Le volume du tronc de cône est égal à la différence des volumes V1 et V2, soit:

686 π/3 cm³ - 18 π = 632 π/3.

Volume du tronc de cône = 632 π/3 cm³.

Partie B

1. Un premier récipient a la forme du tronc de cône décrit ci-dessus et repose sur sa base de rayon 3 cm.

On désigne par x la hauteur, en cm, du liquide qu’il contient. on admet que le volume V(x) de ce liquide, en cm³, est 18 π[(1 + x/6)³ - 1]



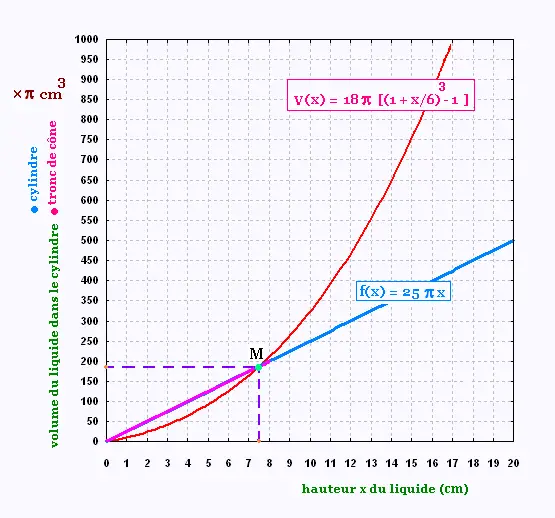
La représentation graphique V(x) montre le volume du liquide dans le tronc en fonction de la hauteur x (sur l’axe des ordonnées, 1 carreau représente 50 x π cm³).

a) Par lecture graphique, une valeur approchée de V(6) est 125 π cm³.

V(6) = 125 π cm³.

b) En utilsant la formule V (6) = 18 π[(1 + 6/6)³ - 1] = 18 π[2³ - 1] = 18 π x 7 = 395.84 ≈ 396.

V(6) = 396 cm³.

2. Un deuxième récipient a la forme d’un cylindre de hauteur 8 cm; ses bases ont pour rayon 5 cm.

a) Volume du cylindre = π (5)² x 8 = 200 π cm³.

b) Pour une hauteur de liquide de x cm, son volume est
π (5)² x = 25 π x cm³

3. L'abscisse du point d'intersection M des deux courbes est comprise entre 7 cm et 8 cm. Son ordonnée est comprise entre 150 π cm³ et 200 π cm³.

4. Pour la valeur de x = 7.5, le tronc de cône contient la même quantité de liquide que le cylindre.

Pour des valeurs de x supéieures à 7.5 cm, le tronc de cône contient plus de liquide que le cylindre.