Mathématiques: Le brevets
Brevet des collèges
Amérique du Nord
juin 2007.
Activités numériques
Exercice 1
1.
A = 2/7 - 15/7 + 5/4 = - 13/7 + 5/4 =
- 52/28 + 35/28 = - 17/28
2.
B = (4 x 105 x 15 x 10-3)/(80 x 10- 1)
=
(4 x 15/80) x 105 - 3 + 1 = 7.5 x 102
3.
C = √75 + 4√27 - 5√48 =
5√3 + 12√3 - 20√3 = - 3√3
4.
D = (2 + 4√5)(2 - 4√5) = 4 - 16x5 = 4 - 80 = - 76
Exercice 2
E = (3 x + 2)2 - (3x + 2)(x + 7)
1.
E = (9 x2 + 12 x + 4 ) - (3x2 + 21 x + 2 x + 14) =
9 x2 + 12 x + 4 - 3x2 - 23 x - 14 =
6 x2 - 11 x - 10 .
E = 6 x2 - 11 x - 10
2.
(3 x + 2)(3 x + 2 - (x + 7)) = (3 x + 2)(3 x + 2 - x - 7) =
(3 x + 2)(2 x - 5)
E = (3 x + 2)(2 x - 5)
3.
E(1/2) = (3/2 + 2) x (1 - 5) = (7/2) x (- 4) =
7 x (- 2) = - 14.
E(1/2) = - 14
.
4.
(3 x + 2)(2 x - 5) = 0
x = - 2/3 ou x = 5/2
Exercice 3

1.
Remise de 20% sur 120.4 $ = 24.08 $
Après cette remise, le montatnt de la facture est:
120.4 - 24.08 = 96.32 $.
2.
Dans des sachets identiques, on répartit 301 caramels
et 172 chocolats .
a) Le nombre maximal de sachets reéalisables
est égal au pgcd (301, 172).
301 = 7 x 43
172 = 4 x 43
pgcd (301, 172) = 43
3.
Dans un sachet, nous aurns donc 7 caramels
et 4 chocolats.
Activités géométriques
Exercice 1
3.
AMB est un triangle de côté [AB] diamètre du
cercle de centre O.
AB = 6 cm
M est un point sur le cercle tel que BM = 4.8 cm.
1.
D'après la propriété:
Si un triangle est défini par le diamètre d’un cercle et un autre
point du cercle, alors ce triangle est rectangle
,
le triangle AMB est rectangle en M.
2.
cos(∠ABM) = = BM/AB = 4.8/6 = 0.8 . D'où :
cos-1(0.8) = 37°
mes(∠ABM) = 37° .
3.
L'angle ∠AOM est l'angle au centre qui
intercepte le même arc que l'angle inscrit ABM.
Donc mes(∠AOM) = 2 mes(∠ABM) = 2 x 37 = 74°
mes(∠AOM) = 74° .
Exercice 2
SABCD est une pyramideà base rectangulaire ABCD
de hauteur [SA].
SA = 15 cm, AB = 8 cm et BC = 11 cm.
1.
Le volume V1 de la pyramide SABCD est égal à
(1/3) x AB x BC x SA = (1/3) x 8 x 11 x 15 = 440 cm3.
V1 = 440 cm3.
2.
[SA] est perpendiculaire à [AB]. D'après le théorème
de Pythagore,
SB2 = AB2 + AS2 = 82 + 153 =
64 + 225 = 289 = 172. Donc:
SB = 17 cm
SB = 17 cm.
3.
SE = 12 cm, SF = 13.6 cm
On calcule les rapports suivants:
SE/SA = 12/15 = 4/5, et
SF/SB = 13.6/17 = 0.8 = 8/10 = 4/5
Ainsi
SE/SA = SF/SB . D'après le théorème réciproque
de Thalès, les droites (EF) et (AB) sont parallèles.
4.
On coupe la pyramide SABCD par le plan pasant par
E parallèlement à la base ABCD. La pyramide SEFGH
est une réduction de la pyramide initiale
SABCD.
a) Le coéfficient de réduction est égale à
(4/5)3 = 64/125
Coéfficient de réduction = 64/125 .
b)
V1/V2 = 64/125. Ou
V1 = (64/125) x V2
V2 = (125/64) x V1.
Exercice 3
Problème
Partie A
1.
L'établissement du groupe 1 : situé à 250 km du musée.
Le car a quité le collège à 7 h 25 mn et roule à la vitesse
moyenne de 100 km/h.
Le temps mis pour parcourir la distance de 250 km est égal
à 250 x 1/100 = 2.50 heures = 2 heures + 0.50 heure =
2 h + 0.50 x 60 mn = 2 h 30 mn.
L'heure d'arrivée est égale à (7 h 25 mn ) + (2 h 30 mn) =
9 h 55 mn.
L'heure d'arrivée est égale est 9 h 55 mn.
.
1.
L'établissement du groupe 2: situé à 120 km du musée.
Le temps mis pour parcourir cette distance de 120 km est égal
à 9 h 30 - 8 h 00 mn = 1 h 30 mn = 1 h 30 (h/60) =
1 h 0.5 h = 1.5 h.
La vitesse moyenne du car est dnc 120 km/1.5 h =
80 km/h
La vitesse moyenne du car = 80 km/h
.
Partie B
Pour travailler dans le musée, deux possibilités d'indemnisation
sont proposées:
Somme d'argent S1: 8 € par heure,
Somme d'argent S2: versement de 90 € en début de mois, puis
5 € par heure.
1.
Voir tableau.
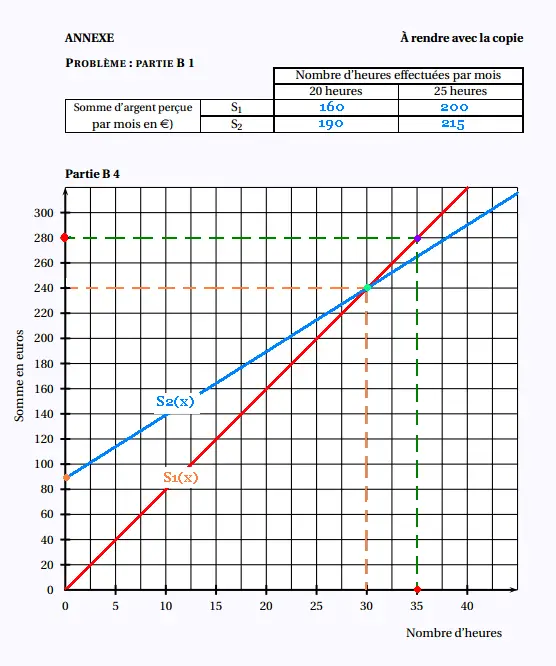
2.
S1(x) = 8 x
S2(x) = 5 x + 90
3.
L'équation : 8 x = 5 x + 90 s'ecrit:
8x - 5x = 90. D'où x = 90/3 = 30.
x = 30
Cette solution correspond au nombre d'heures pour lequel
les deux modes d'indemnisation sont donneront la même
somme d'argent qui est de 240 €.
4.
Voir graphique.
5.
a) et b) Voir graphique.
5.
J'usqu'à 30 heures par mois de travail dans ce musée,
le mode S1 de payement est lus avantageux. Au delà
de 30 jours, c'est le mode S2 qui est le plus avantageux.
|