Mathématiques: Le brevets
Brevet des collèges
Amérique du Nord 10 juin 2010.
Activités numériques
Exercice 1
1.
84 = 22 x 3 x 7
126 = 2 x 32 x 7
84/126 = 22 x 3 x 7/2 x 32 x 7 = 2/3.
2.
(6 x 1012 x 35 x 10-4)/(14 x 103) =
(6 x 35/14) x 1012 - 4 - 3 = 3 x 5 x 1012 - 4 - 3 =
15 x 105 = 1.5 x 106.
3.
√(20) - √(152 x 5) + 2√(45) =
√(4 x 5) - √(152 x 5) + 2√(9 x 5) =
2√(5) - 15√(5) + 6√(5) = (2 - 15 + 6)√(5) =
- 7√5.
4.
17.30 x = 14.80 x + 15
17.30 x - 14.80 x = 15
2.5 x = 15
x = 15/2.5 = 6 cartouches d'encre.
5.
(2x - 3)2 = 4x2 - 12 x + 9.
6.
√(5 + 3) - 6√(11) = √(8) - 6√(11) =
2.828 - 6 x 3.317 = 2.828 - 19.90 = - 17. 07 =
- 17.1.
7.
(7x + 2)2 - 25 = (7x + 2)2 - 52 =
(7x + 2 - 5)(7x + 2 + 5) = (7x - 3)(7x + 7) =
7(7x - 3)(x + 1).
Exercice 2
Deux boîtes: B1 et B2.
Dans B1: 40 vis à bout rond et 60 vis à bout plat.
Total des vis = 40 + 60 = 100 vis.
Dans B1: 38 vis à bout rond et 12 vis à bout plat.
Total des vis = 38 + 12 = 50 vis.
1.
L'électricien prend au hasard une vis de la boîte B1. La
probabilié que cette vis soit à bout rond est égale à 40/100 =
4/10 = 2/5.
2.
L'électricien a remis la vis dans la même boîte.
Il prend au hasard une vis de la boîte B1, puis une vis
de la boîte B2.
1.
R pour rond, et P pour plat, les différents tirages possibles sont:
(R,R) (R,P),(P,R),(P,P).
2.
Le probabilités correspondantes sont:
P(R,R) = (40/100) x (38/50) = (2/5) x (19/25) = 38/125
P(R,P) = (40/100) x (12/50) = (2/5) x (6/25) = 12/125
P(P,R) = (60/100) x (38/50) = (3/5) x (19/25) = 57/125
P(P,P) = (60/100) x (12/50) = (3/5) x (6/25) = 18/125
La probabilité d'obtenir deux vis différentes est égale à :
12/125 + 57/125 = 69/125 = 0.55 > 1/2.
Il y a donc plus d'une chance sur deux d'obenir
deux vis différentes.
Activités géométriques
Exercice 1
Tige d'acier pleine de forme cylindrique de longeur
1.5 m et de rayon de base 4 cm.
1.
Le volume de la tige est égal à l'aire de la base (π x 42)
multiplié par la hauteur (1.5 m = 150 cm). Soit :
π x 42 x 150 = π x 16 x 150 =
7539.82 cm3 = 7540 cm3.
2.
La masse volumique de l'acier est de 7.85 g/cm3.
Ainsi la masse de cette tige est égale à 7540 x 7.85 =
59187.60 g = 59187.60 g ≈ 60 kg.
Exercice 2
1.
270 = 2 x 33 x 5
330 = 2 x 3 x 5 x 11
le pgcd de deux entiers est égal au produit de
leurs facteurs premiers communs affectés de leur plus
petit exposant.
pgcd(270,330) = 2 x 3 x 5 = 30.
2.
Les dimensions d'une plaque sont donc 30 cm x 30 cm.
Le nombre des ces plaques est 270/pgcd x 330/pgcd =
9 x 11 = 99 plaques.
Exercice 3
1.
AC2 = 1402 = 19600.
AB2 + BC2 = 1152 + 802 =
13225 + 6400 = 19625.
AC2 ≠ AB2 + BC2. Donc
le triangle ABC n'est pas rectangle.
2.
cos(CAD) = CD/AC = 100/140 = 0.714 .
cos-1(o.714) = 44.4°
mes(∠ACD) = 44.4°.
3.
Les droites (FC) et (EC) sont sécantes en C.
CD/CE = CD/(CD + DE) = 100/(100 + 20) = 100/120 = 5/6
CA/CF = CA/(CA + AF) = 140/(140 + 28) = 140/168 = 5/6
On trouve donc: CD/CE = CA/CF.
Les rapports de Thalès sont vérifiés. Donc les droites (AD)
et (FE) sont parallèles.
Probleme
Partie 1
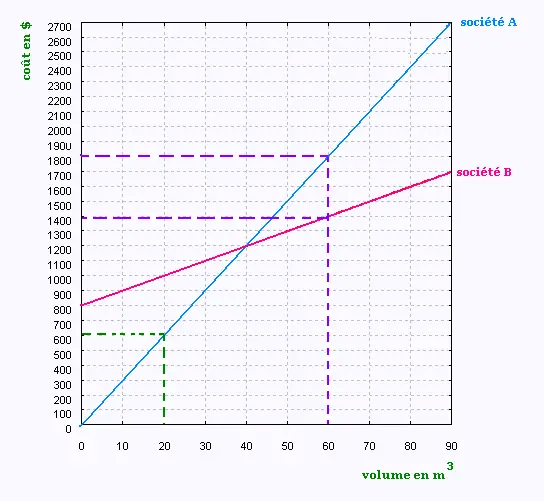
1.
a) À partir du graphique, le coût pour 20 m3 est 600 $.
b) Il existe une relation de proportionnalité entre le
coût et le volume à transporter. Le coéfficient de
proportionnalité correspondant est égal à 30.
Pour l'entrepise A:
Si x est le volume à déménager en m3 , g(x) est le
coût du déménagement. g(x) est l'image de x par la fonction g:
g(x) = 30 x
2.
Pour l'entrepise B:
Si x est le volume à déménager en m3 , f(x) est le
coût du déménagement. f(x) est l'image de x par la fonction f:
f(x) = 10 x + 800
a) f(80) = (10)(80) + 800 = 800 + 800 = 1600.
f(80) = 1600 représente le prix à payer en $ pour un volume
de 80 m3 à transporter par la société B.
b) L'antécédent de 3500 par la fonction f s'obtient par
l'équation:
3500 = 10 x + 800 . D'où x = (3500 - 800)/10 = 350 - 80 =
270 m3.
c) La fonction f est représentée sur un même graphique
que celui de g.
3.
Pour un volume de 60 m3, l'entreprise A demande
1800 $ et l'entreprise B demande 1400 $. Soit une différence de
400 $. Donc la compagnie B charge moins cher.
Partie 2
1.
Le trajet de la maison au chantier est de 442km.
10 h + 2 h 30 + 80 mn + 1h 45 mn =
10 h + 2 h 30 mn + 1 h 20 mn + 1h 45 mn =
14 h 95 mn = 15 h 35 mn.
Partant à 10h h00, M. Dubois arrive au chantier à 15 h 35.
2.
Le camion a roulé pendant 6 h 30 mn = 6.5 heures pour
parcourir le trajet de 442 km.
La vitesse moyenne du camion est donc 442 km/6.5 h = 68 km/h.
|