Mathématiques: Le brevets
Brevet des collèges
Amérique du Nord 7 juin 2011.
Activités numériques
Exercice 1
Trois nombres entiers relatifs consécutifs
rangées dans l'ordre croissant sont choisis
par le professeur:
x, x + 1 et x + 2.
Calcul de Leslie: Le produit du troisième nombre par le double du premier
est égal à (x + 2) (2x ) = 2x( x + 2).
Calcul de Jonathan: Le carré du deuxième nombre est (x + 1)2.
On lui ajoute 2 et on obtient: (x + 1)2 + 2.
1.
a.
L'ecriture de Leslie: 11 x (2 x 9) donne 11 x 18 = 198.
L'ecriture de Lonathan: 102 + 2. donne 100 + 2 = 102.
b.
Dans ce cas le chois du professeur était x = 9. Ainsi
les nmbres choisis sont 9, 10, et 11.
2.
Le professeur choisi maintenant 3 nouveaux entiers: Le
calcul de Leslie et le calcul de Jonathan donnent le même
résultat.
Celà veut dire que 2x(x + 2) = (x + 1)2 + 2
a. Le deuxième nombre est égal à x + 1.
Si x + 1 = 6 , donc x = 5 et
Calcul de Leslie: (2)(5) (5 + 2) = (2)(5)(7) = 70 , et
Calcul de Jonathan: (5 + 1)2 + 2 = 36 + 2 = 38
Ls résultats sont différents. Le professeur n'a pas
choisi 6 comme deuxième nombre.
b.
Si x + 1 = - 7 , donc x = - 8 et
Calcul de Leslie: (2)(- 8)(- 8 + 2) = (2)(- 8)(- 6) = 96 , et
Calcul de Jonathan: (- 8 + 1)2 + 2 = 49 + 2 = 51
Ls résultats sont différents. Le professeur n'a pas
choisi -7 comme deuxième nombre.
c.
Arthur fait le calcul suivant:
• Il prend pour inconnue le deuxième nombre entier.
• Il l'appelle n.
• Il trouve que les nombres consécutifs qu'il cherche sont donc:
n - 1, n et n + 1.
• Il fait les deux calculs:
Le calcul de Leslie est (2)(n - 1)(n + 1) ,
Le calcul de Jonathan est: n2 + 2 .
• Ces résultats doivent être les mêmes, il forme
donc l'équation:
(2)(n - 1)(n + 1) = n2 + 2
• Il développe les deux membres de l'équation en utilisant
l'indentité remarquable de la différence des carrés:
(n - 1)(n + 1) = n2 - 1. Il obtient:
(2)(n - 1)(n + 1) = n2 + 2
2(n2 - 1) = n2 + 2
2n2 - 2 = n2 + 2
2n2 - n2 = 2 + 2
• Il réduit et il obtient:
n2 = 4.
• Il résoud cette équation et trouve:
n = + 2 ou n = - 2.
• Il calcul ainsi les valeurs des nombres choisis:
Pour n = 2, il ecrit les nombres consécutifs
1, 2, et 3.
Pour n = - 2, il ecrit les nombres consécutifs
- 3, - 2, et - 1.
Exercice 2
La lumière parcourt en 1 seconde 300 000 km.
1.
D'un satellite à la terre, elle met 1/75 de seconde.
La distance qui sépare le satellite à la terre est donc:
(1/75 sec) x (300 000 km/sec) = 4000 km.
2.
Du soleil à la terre, elle met 8 mn 30 s = 8 x 60 + 30 = 510 s.
La distance qui nous sépare du soleil est donc égale à :
510 s x 300 000 km/s = 153 000 000 km.
En écriture scientifique: 1.53 x 108 km.
Exercice 3
1.A
On développe l'expression en utilisant l'indentité remarquable
de la différence des carrés:
(x + 1)2 - 9 = (x + 1)2 - 32 =
(x + 1 - 3)(x + 1 + 3) = (x - 2)(x + 4)
2.B
5n x 5m = 5n + m
3.C
On respecte la priorité des opération: d'abord la division
et ensuite la sustraction:
(7/3) - (4/3)÷(5/2) = (7/3) - (4/3) x (2/5) =
(7/3) - (8/15) = (35/15) - (8/15) = 27/15
4.B
774 et 338 sont divisibles tous les deux par 2
puisqu'ils se terminent par 2, 4, 6, ou 8. Ils ne sont pas premiers
entre eux.
63 = 32 x 7 et 44 = 22 x 11 n'ont aucun
diviseur commun. Ils sont donc premiers entre eux.
1035 et 774 sont tous les deux divisibles par 9 parce que la somme
de leurs chiffres est divisibles par 9. Ils ne sont pas premiers entre eux.
5.C
1.52 x 103 est la seule expression qui respecte
la notation scientifique.
Activités gémétriques
Exercice 1
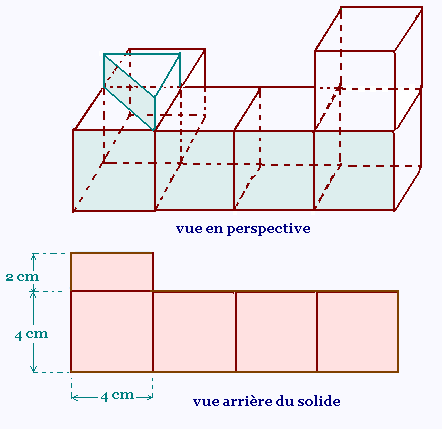
1.
Vue de l'arrière du solide:
2.
Le volume du solide est égal à:
V = volume des 6 cubes + volume du prisme =
6 x (4 x 4 x 4) + (1/2) x (4 x 4 x 2) = 6 x 64 + 16 =
400 cm3.
3.a.
Ce prisme droit est un prisme à base triangulaire. La surface
triangulaire est la seule surface qui a une surface qui lui est
égale et parallèle.
3.b.
∠B est un angle droit. En applicant le théorème de
Pythagore dans le triangle rectangle ABC, on trouve:
AC2 = AB2 + BC2
Nous avons AB = BC = 4 cm, puisque les segments [AB] et
[BC] sont les arrêtes du cube.
Ainsi AC2 = 2AB2. D'où AC = AB √2 =
4√2 cm.
3.c.
L'aire de la face rectangulaire ACFD est égale à
AC x CF = 4 √2 cm x 2 cm = 8√2 cm2
= 1131 mm2.
Exercice 2
1.
On cherche la valeur exacte de la distance BC.
The théorème de Pythagore permet d'ecrire:
BA2 = BC2 + CA2. D'où:
BC2 = BA2 - CA2 =
302 - 252 = 900 - 625 = 275 = 11 x 25
Donc BC = 5√11 cm.
2.
On cherche la valeur de la distance BD au mm près.
BD = BC + CD
CD/AC = tg(49°). D'où CD = 25 tg(49°) =
25 x 1.150 = 28.7592 cm.
Ainsi
BD = 5√11 + 25 tg(49°) = 16.5831 + 28.7592
= 45.342 cm = 453 mm.
BD = 453 mm.
Exercice 3
Les droites (SA) et (OK) sont parallèles.
On sait que SA = 5 cm, OA = 3.8 cm, OR = 6.84 cm, et KR = 7.2 cm.
1.
Calculer la mesure du segment [AR]
AR = OR - OA = 6.84 - 3.8 cm = 3.04 cm.
AR = 3.04 cm.
2.
Calculer la mesure du segment [OK]
Les droites (OR) et (KR) sont sécantes en R.
Les droites (SA) et (OK) sont parallèles.
Le théorème de Thalès s'ecrit:
RA/RO = AS/OK. D'où OK = AS x RO/RA = 5 x 6.84/3.04 = 11.25 cm.
OK = 11.25 cm.
3.
Calculer le périmètre du triangle KRO
P = KR + RO + OK = 7.2 + 6.84 + 11.25 = 25.29 cm
Périmètre du triangle KRO = 25.29 cm.
Problème
Le théatre reçoit environ 500 spectateurs quand le prix
d'une place est de 20$.
Chaque réduction de 1$ du prix d'une place attire 50
spectateurs de plus.
Partie 1
1. Tableau 1
Réduction
en $ | prix de la
place (en $) | nombre de
spectateurs | recette du
spectacle en $ |
| 0 | 20 | 500 | 20 x 500 = 10 000 |
| 1 | 19 | 500 + 50 = 550 | 19 x 550 = 10 450 |
| 2 | 18 | 500 + 2 x 50 = 600 | 18 x 600 = 10 800 |
| 4 | 16 | 500 + 4 x 50 = 700 | 16 x 700 = 11 200 |
2. Tableau 2
Réduction
en $ | prix de la
place (en $) | nombre de
spectateurs | recette du
spectacle en $ |
| x | 20 - x | 500 + x . 50 | (20 - x)(500 + 50 x) |
3.
(20 - x)(500 + 50 x) = 50(20 - x)(10 + x) = 50(200 + 20 x - 10 x - x2) =
50(200 + 10 x - x2) = 10 000 + 500 x - 50x2
R(x) = 10 000 + 500 x - 50x2
Partie 2
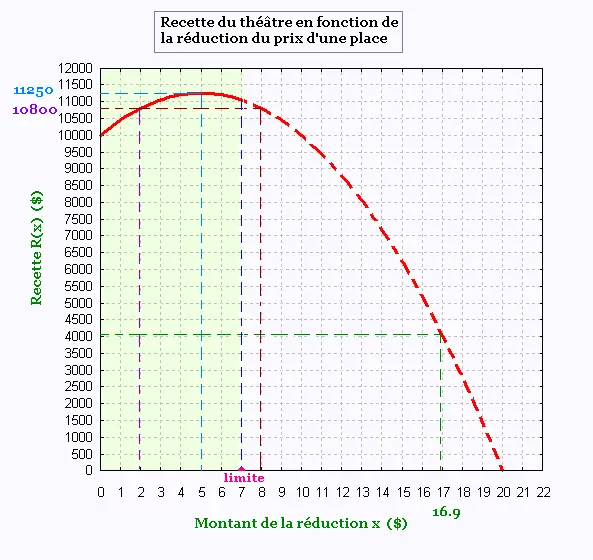
1.
Une réduction de 2 $ correspond à une recette de 10 800 $.
2.
le montant de la réduction correspondant à une recette de 4050 $
est environ 17 $.
3.
L'image de 8 par la fonction R(x) est:
R(8) = 10 000 + 500 x 8 - 50 x 82 =
10 800 $.
Pour une réduction de 8 $ du prix d'une place, comme pour la réduction
de 2 $, la recette du théâtre est de 10 800 $.
4.
La recette maximale correspond à une réduction de 5 $. Cette
recette maximale est de 11 250 $.
Partie 3
La largeur des allées est de 2 m.
On peut placer en moyenne 1.8 sièges par m2.
On veut calculer le nombred eplaces disponibles dans ce
théâtre.
L'aire des deux quarts de disque est:
2 x (1/4) π 132 = 265.46 m2.
La petite base d'un trapèze est égale à (16 - 2)/2 = 7 m.
L'aire des deux trapèzes est 2 x (13 + 7) x 10/2 = 200 m2
L'aire totale de la zone des sièges est égale à la somme de
l'aire des deux quarts de disques et de celle des deux trapèzes:
265.46 m2 + 200 m2 = 465.46 m2
Le total des sièges est donc 465.46 x 1.8 = 837.83 sièges.
Le nombre de places disponibles dans ce théâtre est 838.
Le nombre de places dues à des réductions est égal à:
838 - 500 = 338 places
Ce qui correspond à une limite de 338 /50 = 6.76 ≈ 7 $
de réduction au maximum.
|