Mathématiques: Les brevets

Brevet des collèges     Amérique du nord     juin 2006.

Activités numériques

Exercice 1

1.
A = (3/5 - 1/2) x 5/2 ,
et
B = 16 x 10^{- 1} x 2/(10³)² x 10^{- 8} x 80

a) A = (3/5 - 1/2) x 5/2 = 1/10 x 5/2 = 1/4

b) B = 16 x 10^{- 1} x 2/(10³)² x 10^{- 8} x 80 =
4 x 10^{- 1}/10⁶ x 10^{- 8} x 10 =
4 x 10^{- 1 - 6 + 7} = 4

c) B n'est pas l'opposé de A. B est l'inverse de A.

2.
C = 2√24 + √96 - √600
et
D = (√3 - √2)(√3 + 5√2)

a)
C = 2√4x6 + √16x6 - √100x 6 =
4√6 + 4√6 - 10 √6 = -2√6

b)
D = 3 + 5√6 - √6 - 10 = - 7 + 4√6 .

Exercice 2

1.
E = 4x² + 8x - 5.

E(0.5) = 4 x 1/4 + 8 x 1/2 - 5 = 1 + 4 - 5 = 0

2.
F = (2x + 2)² - 9

a) F = 4x² + 8x + 4 - 9 = 4x² + 8x - 5.

b) F = (2x + 2 - 3)(2x + 2 + 3) = (2x - 1)(2x + 5)

3.
a) (2x - 1)(2x + 5) = 0 donne x = 1/2 ou x = - 5/2
S = {- 5/2, 1/2}

b) Les valeurs de x qui annulent E sont:
x = 1/2 et x = - 5/2

Exercice 3

1.
a) si x = 60, alors:
(2.5)(60) - 75 = 150 - 75 = 75

75 ≯76 . Ainsi 60 n'est pas solution de l'inéquation considérée.

b) 2.5 x - 75 > 76
x >(75 + 76)/2.5 = 60.4
S = {x: x > 60.4}

2.


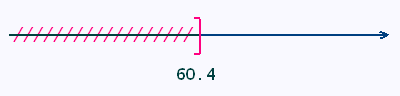
2.
On a les données suivantes:

Dépenses = 75 €
x nombres de glaces à vendre
Une glace coûte 2.5 €
Bénéfice minimum: 76 €

Pour faire un bénéfice minimum de 76 €, avec des dépenses de 75 €, on doit vendre au minum x tel que:

2.5 x - 75 > 76

D'où x > 60.4. C'est à dire x ≥ 61.

On doit vendre au minimum 61 glaces pour faire ce profit minimum de 76 €.

Activités géométriques

Exercice 1

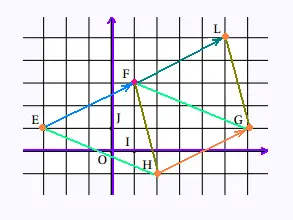
1.

$\color{brown}{a. \; \; E\begin{bmatrix} -3\\ 1 \end{bmatrix} \text { et } F\begin{bmatrix} 1\\ 3 \end{bmatrix} \text { }\\ }$

$\color{brown}{b. \; \; \overrightarrow{EF} \begin{bmatrix} 1 - (- 3) = 4\\ 3 - 1 = 2 \end{bmatrix} \text { }\\ }$

2.
$\color{brown}{ \text {a. } \; \overrightarrow{FL} \begin{bmatrix} 4\\ 2 \end{bmatrix} \text { et } \overrightarrow{HG} \begin{bmatrix} 4\\ 2 \end{bmatrix} }$

$\color{green}{ \text {b. FLGH est un parallélogramme selon la propriété:} \text { }\\ \text { Si } \overrightarrow{FL} = \overrightarrow{GH} \text {, alors FLGH est un parallélogramme . } }$


3.

$\color{blue}{ \overrightarrow{EF} = \overrightarrow{FL} \text { , } \text {donc F est le milieu du segment [EL]. }\\ \text { }\\ }$
4.

$\color{maroon}{ \overrightarrow{EF} = \overrightarrow{FL} \text { et } \overrightarrow{FL} = \overrightarrow{HG} \text { donc } \overrightarrow{EF} = \overrightarrow{HG} \text { }\\ \text {Ainsi EFGH est un parallélogramme. }\\ \text { }\\ \text { Il vient donc: } \overrightarrow{FL} + \overrightarrow{EH} = \overrightarrow{EF} + \overrightarrow{EH} = \overrightarrow{FG} }$

Exercice 2

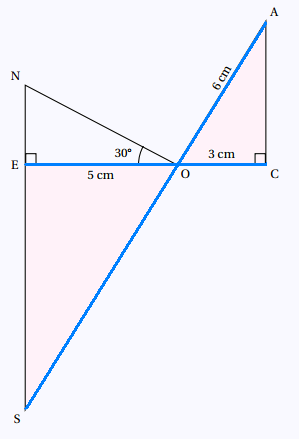
1. ACO est un triangle rectangle en C. D'après le théorème de Pythagore:

AC² = AO² - OC² =
6² - 3² = 36 - 9 = 27 = 3 x 9.
D'où AC = √(3x9) = 3√3.

AC = 3√3 cm .

2.
a.
Les droites (EC) et (AS) sont sont sécantes en O. Elles forment avce les droites (AC) et (NS) des angles alternes-internes égaux à 90° (∠ACO et ∠AEO sont droits). Il en resulte que les droites (AC) et (NS) sont parallèles.

b)
Les droites (EC) et (AS) sont sont sécantes en O. Les droites (AC) et (NS) sont parallèles. Le théorème de Thalès permet alors d'ecrire:

OC/OE = OA/OS= AC/ES

D'où

3/5 = 6/OS = 3/ES
OS = 5 x 6/3 = 10
ES = 3 x 5/3 = 5

OS = 10 cm et ES = 5 cm

3.
On a:
mes(∠NOE) = 30°
cos(∠NOE) = √3/2 = 5/ON

D'où ON = 2 x 5/√3 = 10/√3 = 5.77 cm = 58 mm.

4.
a.
cos(∠COA) = 3/6 = 1/2 . D'où mes(∠COA) = 60°

mes(∠COA) = 60°

Nous avons: mes(∠NOE) + mes(∠EOS) = 90° .

Donc l'angle ∠NOS est droit.

Ainsi le triangle NOS est rectangle en O.

Problème

Parie 1

1. Le saladier a la forme d'une demi-sphère.

Le volume de la demi-sphère est (1/2) x (4/3)π(rayon)³ = (1/2) x (4/3)π12³ = (2/3)π 3 x 4 x 4² = 1152π.

Le volume de la demi-sphère est égal à 1152π cm³ ≈ 3620 cm³

2. Un volume de 1.5 litres est égal à 1.5 dm³ = 1.5 x 1000 cm³ = 1500 cm³

Le saladier de volume 3620 cm³ peut bien contenir 1.5 litres de lait.

Parie 2

Un saladier coûte 5.50 €.

1. 800 saladiers coûtent 800 x 5.50 = 4400 €.

2.
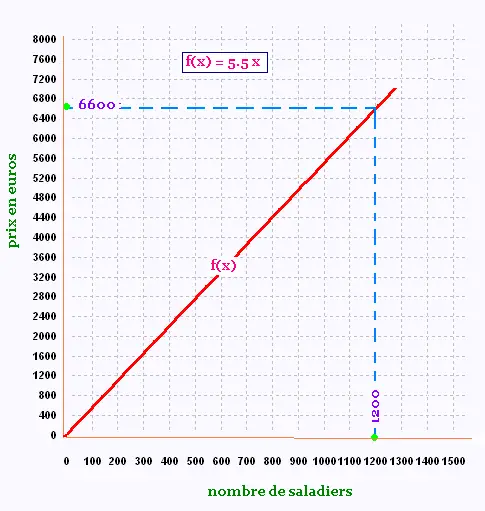
a) Si x est le nombre de saladiers achetés par
le supermarché, alors f(x) = 5.50 x est le prix à payer.

b) Si le supermarché paye 6600 €,
alors il a acheté 6600/5.5 = 1200 saladiers.

c) Graphique:

Parie 3

Sofia a vendu 220 saladiers, Natacha 200, Lorie 290, Magali 250.

1. En tout, il a été vendu :

220 + 200 + 290 + 250 = 960 saladiers.

En tout, il a été vendu 960 saladiers.

2.
Natacha a vendu 200 saladiers. Ça représente 200/960 = 0.2083 = 20.8% du stock.

Natacha a vendu 20.8% du stock de saladiers.

1. Le supermarché a vendu 80% de son stock qui est égal à 960 saladiers.

80% x = 960. D'où x = 960 x 100/80 = 1200 saladiers.