Mathématiques: Les brevets
Brevet des collèges
Amérique du sud
novembre 2003
Activités numériques
Exercice 1
A = (3x - 1)2 - (3x - 1)(2x + 8).
1. Développer et réduire A.
A = 9x2 - 6 x + 1 - (6 x2 + 24 x - 2x - 8) =
9x2 - 6 x + 1 - 6 x2 - 22 x + 8 =
3x2 - 28 x + 9
A = 3x2 - 28 x + 9
2. Factoriser A.
A = (3x - 1)[(3x - 1) - (2x + 8)] =
(3x - 1)[3x - 1 - 2x - 8)] = (3x - 1)[x - 9)
A = (3x - 1)[x - 9)
3. Résoudre l’équation : (3x -1)(x - 9) = 0
x = 1/3 ou x = 9
A = 0 ssi x = 1/3 ou x = 9
Exercice 2
B = 3√5 - 2√45 + √500
C = (√3 + 4)2 - 19
B = 3√5 - 6√5 + 10√5 = 7√5.
B = 7√5
C = 3 + 8√3 + 16 - 19 = 8√3 .
C = 8√3.
Exercice 3
D = (4x + 2)/5
1. Pour x = 3/4 D(3/4) = 1.
Puisque 1 < 3, donc 3/4 est une solution de
l’inéquation (4x + 2)/5 < 3
2. Résolution de l’inéquation (4x + 2)/5 < 3 :
(4x + 2)/5 < 3
4x + 2 < 15
4x < 15 - 2
4x < 13
x < 13/4.
Solutions: x < 13/4.
Représentation des solutions sur une
droite graduée:

Exercice 4
Points marqués d'un basketteur:
• modalité = Nombre de points marqués.
• effectif = Nombre de matchs où ce nombre de
points a été marqué.
• cumulés = effectifs cumulés.
| modalité |
15 | 19 | 20 | 21 | 24 | 25 | 28 | 29 | 32 | 34 | 37 | 42 |
| effectifs |
2 | 3 | 1 | 4 | 3 | 2 | 6 | 1 | 3 | 1 | 2 | 1 |
| cumulés |
2 | 5 | 6 | 10 | 13 | 15 | 21 | 22 | 25 | 26 | 28 | 29 |
Série statistique d'effectif total égal à 29.

1. Calcul de la moyenne:
Moyenne pondérée = (2 x 15 + 3 x 19 + 1 x 20 + 4 x 21 + 3 x 24 + 2 x 25 +
6 x 28 + 1 x 29 + 3 x 32 + 1 x 34 + 2 x 37 + 1 x 42)/29 = 19.48.
Le nombre moyen de points marqués est l'ordre de 20 points.
2. Calcul de la médiane:
Nous avons (29 + 1)/2 = 15. Donc la médiane se situe à la 15ème position,
c'est à dire 25.
La médiane des points marqués est égal à 25 points
Activités géométriques
Exercice 1
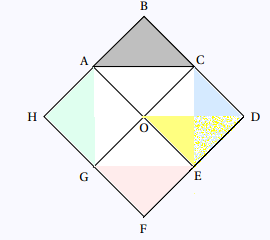
1.
a. L’image du triangle ABC par la symétrie orthogonale d’axe (GC)
est le triangle CDE.
b. L’image du triangle ABC par la rotation
de centre O, d’angle 90° qui amène E en C
est le triangle AHG.
2.
a. Le triangle OCD est l’image du triangle ABC par la translation de
vecteur . .
b. Le triangle GFE est l’image du triangle ABC par la symetrie
centrale de centre O.
Exercice 2
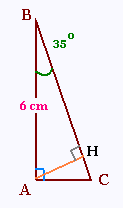 AC/AB = tg(35°)
AC/AB = tg(35°)
AC = AB tg(35°)) = 6 x 0.700 =
4.20 cm = 42 mm.
AC = 42 mm.
AH/AB = SIN(35°)
AH = AB SIN(35°)) = 6 x 0.5736 =
3.44 cm = 34 mm.
H = 34 mm.
Exercice 3
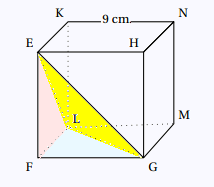
1.
Les faces de la pyramide EFGL:
• 3 triangles rectangles EFG, EFL, et FLG,
• 1 triangle équilatéral ELG de sommet E.
2.
EFL est un triangle isocèle rectangle en F.
3.
Volume de la pyramide EFGL = (aire de la base FLG) x (hauteur EF)/3 =
(9 x 9/2) x (9)/3 = 121.5 cm3.
Problème
Partie A
M est un point du segment [AB].
On pose AM = x. (x est une distance exprimée en mètre).
1.
L'aire du jardin = (DC + AB) x AD /2 =
(70 + 50) x 30/2 = 120 x 30/2 = 60 x 30 = 1800
m2.
L'aire du jardin = 1800 m2.
2.
a. L’aire de AMGD (potager) = x . AD = 30 x m2.
b. L’aire de BCGM (pelouse) est égale à l'aire du
jardin - aire du potager = 1800 - 30 x m2.
3.
a. La pelouse et le potager ont la même aire
si
1800 - 30 x = 30 x
C'est à dire
60 x = 1800 ou x = 1800/60 = 30
x = 30 mètres.
b. on a x = AM = 30 = AD . Ainsi le potager
AMGD est un carré de côté 30 mètres.
Partie B
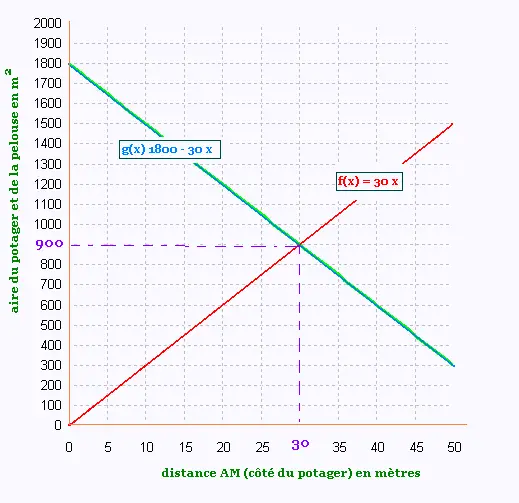
On veut représenter graphiquement la situation de la partie A à l’aide de deux fonctions f et g.
f est définie par: f (x) = 30x pour l’aire du potager AMGD.
g est définie par: g(x) = 1800 - 30x pour l’aire de la pelouse BCGM.
1. Tableau de valeurs
| x |
0 |
10 |
20 |
40 |
50 |
| f(x) |
0 |
300 |
600 |
1200 |
1500 |
| g(x) |
1800 |
1500 |
1200 |
600 |
300 |
2.
Représentation graphique:
Partie C
1. La pelouse, d’une aire de 900 m2,
est ensemencée avec un gazon au prix initial de 0.16 € le m2.
Le vendeur accorde une remise de 5 %.
Prix avant remise = 900 x 0.16 = 144 €
valeur du rabais: 144 x 5% = 7.2 €
Le coût global pour la pelouse après le rabais
est 144 - 7.2 = 136.8 €
coût final pour la pelouse = 136.8 €
2.
Pour 40€, on aurait 50 plants de salade et 40 pieds de tomate.
Pour 50 €, on aurait 25 plants de salade et 60 pieds de tomate.
On veut calculer le prix d’un plant de salade et le prix d’un pied de
tomate.
3.
Système d’équations traduisant ces données:
Soient:
x le prix d’un plant de salade et
y le prix d’un pied de tomate. On a:
|