Mathématiques: Les brevets
Brevet des collèges
Antilles-Guyane
juin 2009.
Activités numériques
Exercice 1
On tire un billet d'un sac contenant exactement
180 billets.
1.
La probabilité de gagner un lecteur MP3 est 4/180 = 1/45.
2.
La probabilité de gagner une peluche (grande ou
petite) est 12/180 + 36/180 = 48/180 = 4/15
3.
La probabilité de ne rien gagner est (180 - 4 - 12 - 36 - 68)/180 =
60/180 = 1/3
Exercice 2
1.
A = (3 x 105 x 4 x (10-3)2)/(16 x 10-4) =
(3 x 4/16) x 105 - 6 + 4 = (3/4) x 103 =
0.75 x 1000 = 750.0 = 7.5 x 102
2.
E = 16 - (5x - 3)2
a) E(-1) = 16 - (5(-1) - 3)2 = 16 - (- 8)2 =
16 - 64 = - 48.
b) E = 16 - (25x2 - 30x + 9) =
16 - 25x2 + 30x - 9 = - 25x2 + 30x + 7.
c)16 - (5x - 3)2 = 42 - (5x - 3)2 =
(4 + 5x - 3)(4 - 5x + 3) = (5x + 1)(- 5x + 7)
3.
a) Un multiple de 5 est un nombre qui se termine par
0 ou 5. La somme de deux multiples de 5 se termine aussi
par 0 ou 5.
La phrase proposée est vraie.
La somme de deux multiples de 5 est un multiple de 5
b) 2 et 3 sont deux diviseurs d'un nombre entier, leur
somme 2 + 3 = 5 n'est pas toujours un diviseur de ce nombre.
2 et 3 sont deux diviseurs du nombre entier 18. Mais
leur somme 2 + 3 = 5 n'est pas un diviseur de ce nombre.
2 et 3 sont deux diviseurs du nombre entier 90.
Leur somme 2 + 3 = 5 est un diviseur de ce nombre.
90 = 2 x 45
90 = 3 x 30
90 = 5 x 18
Exercice 3
1.
pgcd(1394, 255)
Par la méthode de l'algorithme d'Euclide:
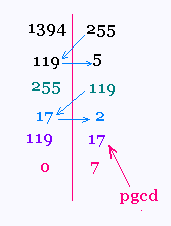
pgcd(1394, 255) = 17.
2.
En utilisant toutes les graines, le maximum de colliers que
l'on peut réaliser est égal au pgcd(1394, 255) = 17.
3.
Chaque collier contiendra:
1394/17 = 82 graines d'açaï, et
255/17 = 15 graines de palmier pêche.
Activités géométriques
Exercice 1
Exercice 2
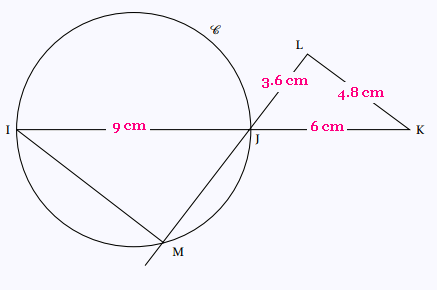
1.
62 = 3.62 + 4.82
D'après le théorème réciproque de Pythagore, le triangle
JKL est rectangle en L.
2.
[IJ] est le diamètre du cercle.
D'après la propriété:
Si un triangle est défini par le diamètre d’un cercle et un autre
point du cercle, alors ce triangle est rectangle
,
le triangle IJM est rectangle en M.
3.
Les angles M et L sont égaux. Ils sont alternes internes
au droites (LK) et (IM). Ainsi ces droites
(LK) et (IM) sont parallèles.
les droites (ML) et (IK) sont sécantes en J.
Le théorème de Thalès s'ecrit:
JL/JM = JK/JI = KL/IM
D'où:
JM = JL x JI/JK = 3.6 x 9/6 = 5.4 cm
JM = 5.4 cm.
Problème
Partie A
1.
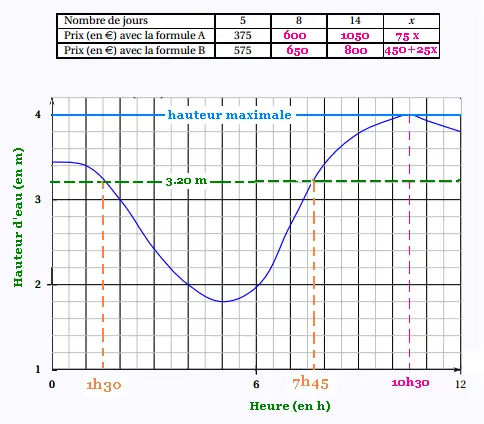
2.
Avec 750 € La formule B permet:
750 = 450 + 25 x. D'où x = (750 - 450)/25 = 12 jours.
3.
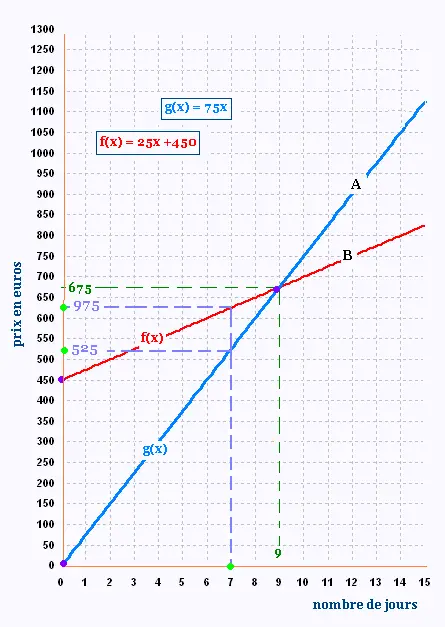
4.
À partir de 9 jours, la formule B est plus avantageuse.
5.
a)
Pour 7 jours, la formule A est plus avantageuse. Le prix correspondant est
525 € au lieu de 975 avec la formule B.
b) Une remise de 5% sur 525 € donne
5% x 525 € = 26.25 € de réduction.
Ces vacances coûteront donc:
525 € - 26.25 € = 498.75 €
Partie B
1.
Les tranches horaires de départs possibles sont,
soit avant 1h30, soit après 7h 45.
2.
Pour la hauteur maximale, le départ se fera à
10h 30.
|