Maths
- 45 -
Les brevets
Sujets
Corrigés
Brevets blancs
© The scientific sentence. 2010
|
Mathématiques: Le brevets
Brevet des collèges
Diplôme national du brevet
Antilles - Guyane juin 2008.
Activités numériques
Exercice 1
1.
A = (2/3 + 1/2)/(17/9 - 1/3)
2/3 + 1/2 = (4 + 3)/6 = 7/6
17/9 - 1/3 = 17/9 - 3/9 = 14/9
A = (7/6)/(14/9) = (7/6) x (9/14) =
(1/2) x (3/2) = (1 x 3)/(2 x 2) = 3/4
A = 3/4.
2.
B = 81 x 103 x 6 x 10- 10/18 x 10-2 =
(81 x 6 /18) x 103 - 10 + 2 = 27 x 10- 5 =
2.7 x 10- 4
B = 2.7 x 10- 4.
Exercice 2
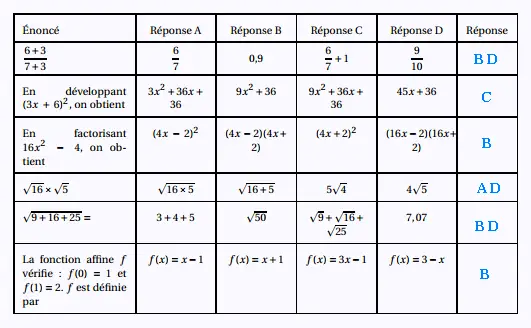
Exercice 3
1.
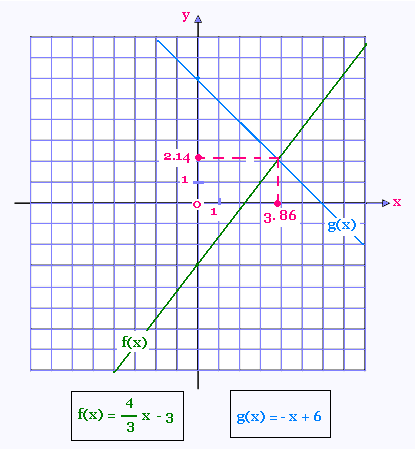
2.
Les coordonnées du point d'intersection K des deux droites
doivent vérifier l'equation f(x) = g(x).
C'est à dire :
(4/3) x - 3 = - x + 6
La solution de cette équation est:
x = 27/7 = 3.86
y = - 27/7 + 6 = 17/7 = 2.14
K(3.86, 2.14).
Activités gémétriques
Exercice 1
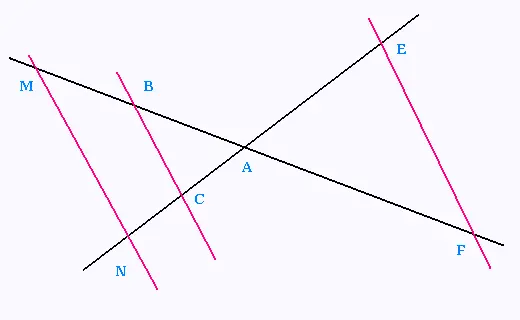
les droites (BC) et (MN) sont parallèles.
AB = 4.5 cm, AC = 3 cm, AN = 4.8 cm , et MN = 6.4 cm
1.
les droites (MF) et (NE) sont sécantes en A.
les droites (BC) et (MN) sont parallèles.
The théorème de Thalès permet d'ecrire:
AB/AM = AC/AN = BC/MN
4.5/AM = 3/4.8 = BC/6.4
D'où:
AM = 4.5 x 4.8/3 = 7.2 cm.
AM = 7.2 cm.
BC = 3 x 6.4/4.8 = 4 cm
BC = 4 cm.
2.
AE = 5 cm , AF = 7.5 cm.
AB/AF = 4.5/7.5 = 3/5
AC/AE = 3/5
On trouve AB/AF = AC/AE. D'après le théorème réciproque de Thalès
le droites (BC) et (EF) sont parallèles.
Exercice 2
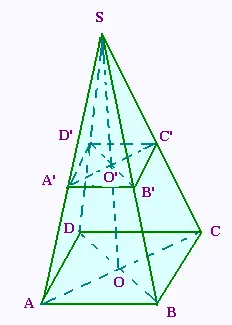 On considère une pyramide régulière SABCD à base
rectangulaire.
On considère une pyramide régulière SABCD à base
rectangulaire.
AB = 40 cm, et BD = 50 cm. La hauteur [SO] mesure 81 cm.
1.
La base de la pyramide est le rectangle ABCD. Le triangle
ABD est rectangle en A. Le théorème de Pythagore permet
d'ecrire: BD2 = AB2 + AD2. D'où:
AD2 = BD2 - AB2 = 502 -
402 = 900.
Donc AD = √900 = 30.
AD = 30 cm.
2.
Le volume de n'importe quelle pyramide d'aire
de base B et de hauteur h est égal à: B x h/3.
V = B x h/3 = AB x AD x SO/3 = 40 x 30 x 81/3 = 32400 cm3.
V = 32400 cm3.
3.
SO' = 54 cm.
On fait une section de la pyramide au niveau
SO' et parallèlement à la base.
a) La section obtenue A'B'C'D' est un rectangle
homoloque au rectangle de base ABCD.
b)
La pyramide SA'B'C'D' est une réduction de la pyramide
initiale SABCD.
Les droites (AS) et (BS) sont sécantes en S.
Les droites (A'B') et (AB) sont parallèles.
Le théorème de Thalès permet d'ecrire:
A'B'/AB = SA'/SA
Les droites (AS) et (OS) sont sécantes en S.
Les droites (A'O') et (AO) sont parallèles.
Le théorème de Thalès permet d'ecrire
SA'/SA = SO'/SO
Ainsi
A'B'/AB = SO'/SO = 54/81 = 2/3
Un même raisonnement conduit à
C'B'/CB = SO'/SO = 54/81 = 2/3
Il volume de la pyramide SA'B'C'D' est donc égal à
A'B' x B'C' x SO'/3
Le coéfficient de réduction est alors égal à :
volume de la pyramide SA'B'C'D'/volume de la pyramide SABCD =
A'B' x B'C' x SO'/AB' x BC x SO = (2/3) x (2/3) x (2/3) = (2/3)3.
Le coéfficient de réduction est égal à (2/3)3.
c)
volume de la pyramide SA'B'C'D' = (2/3)3 x volume de la pyramide SABCD =
(2/3)3 x 32400 cm3 = 9600 cm3.
volume de la pyramide SA'B'C'D' = 9600 cm3.
4.
D'après la propriété
les diagonales d'un rectangle se coupent en
leur milieu et ont même mesure,
on ecrit:
AO = AC/2 = BD/2 = 25 cm.
a)
tan(∠SAO) = SO/OA = 81/25 = 3.24
b)
tan-1 (3.24) = 73°.
Mesure de ∠SAO = 73°.
Problème
1.
2.
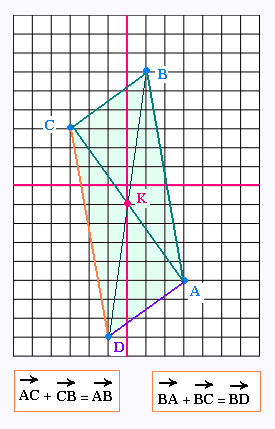
a) Le vecteur AB a pour composantes les différences des
composantes des vecteurs OB et du vecteur OA;
AB = OB - OA = (1,6) - (3, - 5) = (1 - 3, 6 + 5) = (- 2, 11).
Le module du vecteur AB est √((- 2)2 + 112) =
√(4 + 121) = √(125) = 5√5.
AB = 5√5 cm.
De même pour le vecteur AC:
AC = OC - OA = (- 3, 3) - (3, - 5) = (- 3 - 3, 3 + 5) = (- 6, 8).
Le module du vecteur AC = √((- 6)2 + 82) =
√(36 + 64) = √(100) = 10.
AC = 10 cm.
De même pour le vecteur BC:
BC = OC - OB = (- 3, 3) - (1, 6) = (- 3 - 1, 3 - 6) = (- 4, - 3).
Le module du vecteur BC = √((- 4)2 + (- 3)2) =
√(16 + 9) = √(25) = 5.
BC = 5 cm.
b)
AB2 = (5√5)2 = 125
AC2 = 102 = 100
BC2 = 52 = 25
Nous avons donc : AB2 = AC2 + CB2
D'après le théorème réciproqie de Pythagore, le
triangle ABC est rectangle en C.
3.
a) Voir figure
b)
c) D'après la relation de Chasles,
4.
5.
a)
\[\overrightarrow{AB} \times \overrightarrow{AC} = \begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
- 2 & 11 & 0 \\
- 6 & 8 & 0
\end{vmatrix} =
\begin{bmatrix}
11 \times 0 - 8 \times 0 = 0\\
-6 \times 0 - (- 2) \times 0 = 0\\
(- 2) \times 8 - 11 \times (- 6) = 50 \; \;
\end{bmatrix} \]
\[\overrightarrow{AB} \times \overrightarrow{AC} = \begin{bmatrix}
0 \\ 0 \\ 50
\end{bmatrix}\]
Ainsi
L'aire du parallélogramme ABCD est égale à
50 cm2.
b)
K est le centre de symétrie du paralléloramme ABCD. Le point
K est donc le milieu du segment [AC]. Ainsi Ce point
K de coordonnées (x,y) doit satsfaire l'équation:
\[\overrightarrow{AK} = \overrightarrow{KC} \]
C'est à dire :
x - 3 = - 3 - x
y - (- 5) = 3 - y
D'où:
x = 0 et
y = - 1.
K(0, - 1)
Annexe
Une translation est une transformation géométrique qui déplace
ou qui glisse un objet suivant vecteur directeur donné.
Construire l'image d'une figure par une translation
c'est faire glisser dans une direction, un sens et
avec une longueur donnée selon le vecteur de translation.
Propriétés:
• L’image d’une droite, par une translation, est
une droite parallèle.
• La translation conserve le parallélisme, l’orthogonalité et
les angles.
|
|