Mathématiques: Le brevets
Brevet des collèges Grenoble juin 2002.
Activités numériques
Exercice 1
A = (2/7) + (1/7) x (8/3) = (2/7) + (8/21) =
(6/21) + (8/21) = 14/21 = 2/3.
A = 2/3.
B = (√3 - 7)2 = 3 - 14√3 + 49 =
51 - 14√3.
B = 51 - 14√3.
C = √50 + 2√18 = 5√2 + 6√2 =
11√2.
C = 11√2.
Exercice 2
A = (2x - 3)2 - (2x - 3)(x - 2)
1.
A = 4x2- 12x + 9 - 2x2 + 4x + 3x - 6 =
2x2 - 5x + 3
A = 2x2 - 5x + 3.
2.
A = (2x - 3)[(2x - 3) - (x - 2)] =
(2x - 3)(2x - 3 - x + 2) =
(2x - 3)(x - 1).
A = (2x - 3)(x - 1).
3.
A = 0
(2x - 3)(x - 1). = 0 ssi x = 3/2 ou x = 1.
A = 0 ssi x = 3/2 ou x = 1.
4.
A(- 2) = (2(- 2) - 3)((-2) - 1) =
(- 4 - 3)( - 2 - 1) =
(- 7) x (- 3) = + 21.
A(- 2) = 21.
Exercice 3
1.
Les nombres 682 et 496 ne sont pas premiers entre eux;
puisque juste un regard permet de conclure qu'il sont
divisibles par 2.
On rappelle que deux nombres sont
premiers entre eux s'ils n'ont aucun facteur
en commun autre que 1, comme 10 et 21.
2.
Calculons le pgcd de 682 et de 496
à l'aide de l'algorithme d'Euclide:
682 = 1 x 496 + 186
496 = 2 x 186 + 124
186 = 1 x 124 + 62
124 = 2 x 62 + 0
Il faut prendre le dernier reste avant le zéro,
donc pgcd(682, 496) = 62.
pgcd(682, 496) = 62.
3.
682 = 62 x 11
496 = 62 x 8
Donc:
682/496 = 62 x 11/62 x 8 = 11/8.
682/496 = 11/8.
Exercice 4
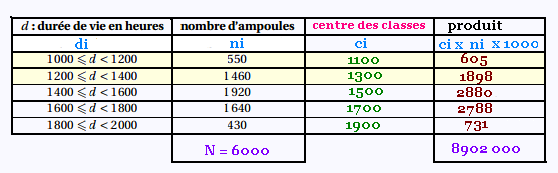
1.
Le pourcentage d'ampoules qui ont une durée de vie de
moins de 1400 heures est (550 + 1460)/6000 = 33.5%.
(partie coloriée en jaune).
2.
La durée de vie moyenne d'une ampoule est
8902 000/6000 = 1484 heures.
Activités géométriques
Exercice 1
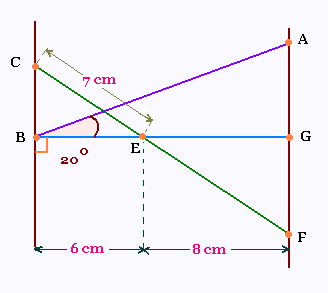
Exercice 2
1.
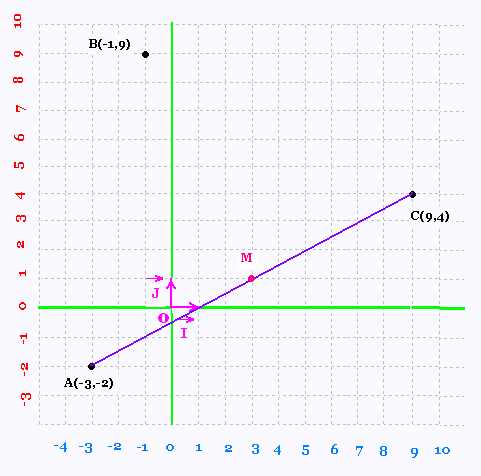
2.
Le point M(x, y) est le milieu du segment [AC].
Donc .
C'est à dire :
x + 3 = 9 - x
y + 2 = 4 - y
ou
x = 3 et y = 1
M(3, 1).
3.
4.
Exercice 3
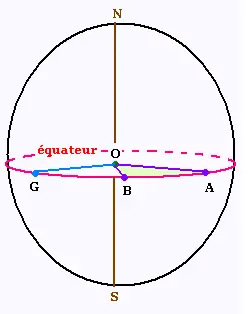
1.
La longeur de l'équateur est égale à 2 x π x 6370 = 40024 km.
2.
Nous avons la proportion suivante:
33°/360° = mes /circonférence.
Donc
mes = 40024 x 33/360 = 3669 km.
Activités géométriques
Partie A
Trajet aller:
durée = 0h 01 mn - 6h 01 mn = 3h
vitesse du train = distance/durée = 542 km/3h = 181 km/h
V-aller = 181 km/h.
Trajet retour:
durée = 21h 58 mn - 19h 04 mn = 2h 54 mn = 2h + 54/60 h = 2.9 h.
vitesse du train = distance/durée = 542 km/2.9h = 187 km/h.
V-retour= 187 km/h.
Partie B
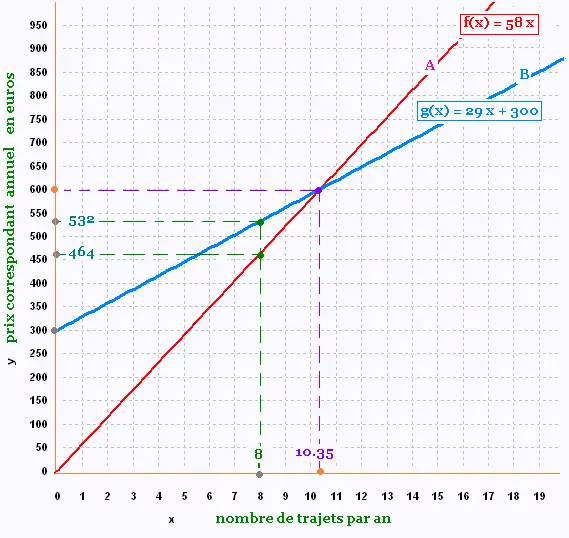
1.
Pour 8 trajets par an, on doit payer:
Avec l'option A: 58 x 8 = 464 €
Avec l'option B: 29 x 8 + 300 = 532 €.
2.
yA = 58 x.
yA = 58 x
3.
Pour l'option B,
On paye un forfait de 300 € par an, et par la suite,
durant toute l'année, le prix d'un trajet ne coûtera que 29 €..
4.
Pour l'option B, le prix total annuel n'est pas prportionnel
aux nmbres de trajets, puisqu'il n'existe pas une constante de
proportionnalité entre eux.
5.
Voire le graphique.
6.
a) À partir de 11 trajets par an, l'option B est
plus avantageuse.
b) 29 x + 300 < 58 x
300 < 58 x - 29 x
300 < 29 x
x > 300/29 = 10.35.
x > 11.
|